题目内容
【题目】已知某公司为郑州园博园生产某特许商品,该公司年固定成本为10万元,每生产千件需另投入2 .7万元,设该公司年内共生产该特许商品工x千件并全部销售完;每千件的销售收入为R(x)万元,
且 ,
,
(I)写出年利润W(万元〉关于该特许商品x(千件)的函数解析式;
〔II〕年产量为多少千件时,该公司在该特许商品的生产中所获年利润最大?
【答案】(1) 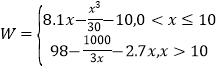 .
.
(2) 当年产量为9千件时,该公司在该特许商品生产中获利最大.
【解析】
分析:(1)根据利润等于收入减去成本得解析式(2)先分段求最大值,一段根据导数得单调性,根据单调性变化规律确定最大值,另一段根据基本不等式求最值,最后取两段最大值的最大值.
详解:
(1)当![]() 时,
时,![]()
当![]() 时,
时,![]()
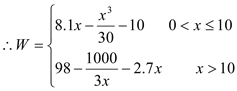
(2)①当![]() 时,由
时,由![]()
当![]()
∴当![]() 时,W取最大值,且
时,W取最大值,且![]()
②当![]() 时,W=98
时,W=98![]()
当且仅当![]()
综合①、②知![]() 时,W取最大值.
时,W取最大值.
所以当年产量为9千件时,该公司在该特许商品生产中获利最大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三 年级一班至六班进行了“本届奥运会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 5 | 9 | 11 | 9 | 7 | 9 |
满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为ξ,求随机变量ξ的分布列及数学期望.