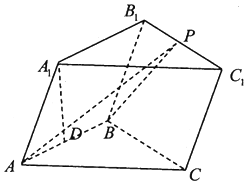
题目内容
【题目】已知函数![]() ,
,![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ).
).
(1)判断曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 的公共点个数;
的公共点个数;
(2)当![]() 时,若函数
时,若函数![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2) ![]()
【解析】分析:(1)根据导数的几何意义可得切线方程,然后根据切线方程与![]() 联立得到的方程组的解的个数可得结论.(2)由题意求得
联立得到的方程组的解的个数可得结论.(2)由题意求得![]() 的解析式,然后通过分离参数,并结合函数的图象可得所求的范围.
的解析式,然后通过分离参数,并结合函数的图象可得所求的范围.
详解:(1)∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
,
∴曲线在点![]() 处的切线方程为
处的切线方程为![]() .
.
由![]() 得
得![]() .
.
故![]() ,
,
所以当![]() ,即
,即![]() 或
或![]() 时,切线与曲线
时,切线与曲线![]() 有两个公共点;
有两个公共点;
当![]() ,即
,即![]() 或
或![]() 时,切线与曲线
时,切线与曲线![]() 有一个公共点;
有一个公共点;
当![]() ,即
,即![]() 时,切线与曲线
时,切线与曲线![]() 没有公共点.
没有公共点.
(2)由题意得![]() ,
,
由![]() ,得
,得![]() ,
,
设![]() ,
,
则![]() .
.
又![]() ,
,
所以当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增.
单调递增.
所以![]() .
.
又![]() ,
,![]() ,
,
结合函数图象可得,当![]() 时,方程
时,方程![]() 有两个不同的实数根,
有两个不同的实数根,
故当![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.

【题目】“微信运动”已成为当下热门的健身方式,小明的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
| 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 |
|
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)若采用样本估计总体的方式,试估计小明的所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数超过8000步时被系统评定为“积极型”,否则为“懈怠型”.根据小明的统计完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 以上的把握认为“评定类型”与“性别”有关?
以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附:![]()
![]()
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】抽样统计甲、乙两名学生的5次训练成绩(单位:分),结果如下:
学生 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
甲 | 65 | 80 | 70 | 85 | 75 |
乙 | 80 | 70 | 75 | 80 | 70 |
则成绩较为稳定(方差较小)的那位学生成绩的方差为 .