题目内容
【题目】定义在[0,+∞)上的函数f(x)满足:①当x∈[1,2)时, ![]() ;②x∈[0,+∞)都有f(2x)=2f(x).设关于x的函数F(x)=f(x)﹣a的零点从小到大依次为x1 , x2 , x3 , …xn , …,若
;②x∈[0,+∞)都有f(2x)=2f(x).设关于x的函数F(x)=f(x)﹣a的零点从小到大依次为x1 , x2 , x3 , …xn , …,若 ![]() ,则x1+x2+…+x2n= .
,则x1+x2+…+x2n= .
【答案】6×(2n﹣1)
【解析】解:∵①当x∈[1,2)时, ![]() ;②x∈[0,+∞)都有f(2x)=2f(x). 当x∈[2,4)时,
;②x∈[0,+∞)都有f(2x)=2f(x). 当x∈[2,4)时, ![]() ∈[1,2),
∈[1,2),
f(x)=2f( ![]() x)=2(
x)=2( ![]() ﹣|
﹣| ![]() ﹣
﹣ ![]() |)=1﹣|x﹣3|,x∈[4,8)时,
|)=1﹣|x﹣3|,x∈[4,8)时, ![]() ∈[2,4),
∈[2,4), 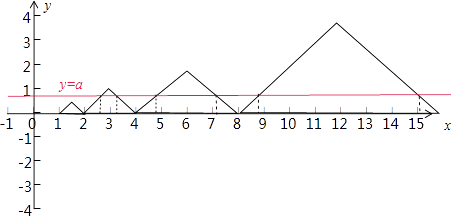
f(x)=2f( ![]() x)=2(1﹣|
x)=2(1﹣| ![]() x﹣3|)=2﹣|x﹣6|,
x﹣3|)=2﹣|x﹣6|,
同理,则 ![]() ,F(x)=f(x)﹣a在区间(2,3)和(3,4)上各有1个零点,分别为x1 , x2 , 且满足x1+x2=2×3=6,
,F(x)=f(x)﹣a在区间(2,3)和(3,4)上各有1个零点,分别为x1 , x2 , 且满足x1+x2=2×3=6,
依此类推:x3+x4=2×6=12,x5+x6=2×12=24…,x2n﹣1+x2n=2×3×2n﹣1 .
∴当 ![]() 时,x1+x2+…+x2n﹣1+x2n=6×(1+2+22+…+2n﹣1)=6×
时,x1+x2+…+x2n﹣1+x2n=6×(1+2+22+…+2n﹣1)=6× ![]() =6×(2n﹣1),
=6×(2n﹣1),
所以答案是:6×(2n﹣1).

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
