题目内容
已知函数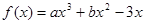 在
在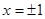 处取得极值,求函数
处取得极值,求函数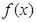 以及
以及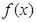 的极大值和极小值.
的极大值和极小值.
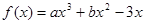 在
在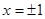 处取得极值,求函数
处取得极值,求函数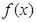 以及
以及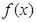 的极大值和极小值.
的极大值和极小值.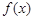 在
在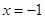 处取得极大值
处取得极大值 ,在
,在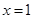 处取得极小值
处取得极小值 .
.试题分析:先求出导函数
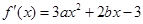 ,进而根据条件得出
,进而根据条件得出 ,列出方程组
,列出方程组 ,从中解出
,从中解出 的值,进而根据函数的极值与导数的关系求解出函数
的值,进而根据函数的极值与导数的关系求解出函数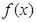 的极大值与极小值即可.
的极大值与极小值即可.试题解析:因为
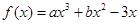 ,所以
,所以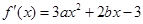
因为函数
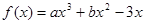 在
在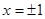 处取得极值
处取得极值所以

即
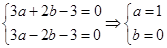
∴
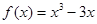 ,
,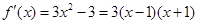
令
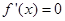 ,得
,得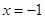 或
或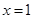
当
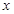 变化时,
变化时,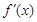 与
与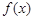 的变化情况如下表:
的变化情况如下表: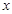 | 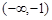 |  | 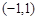 | 1 | 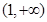 |
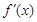 | + | 0 | — | 0 | + |
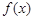 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴
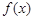 在
在 处取得极大值
处取得极大值 ,在
,在 处取得极小值
处取得极小值 .
.
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
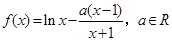 .
.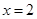 是函数
是函数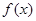 的极值点,求曲线
的极值点,求曲线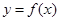 在点
在点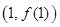 处的切线方程;
处的切线方程;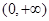 上为单调增函数,求
上为单调增函数,求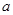 的取值范围;
的取值范围;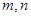 为正实数,且
为正实数,且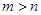 ,求证:
,求证: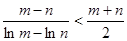 .
. (如图所示,其中O为圆心,
(如图所示,其中O为圆心,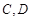 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).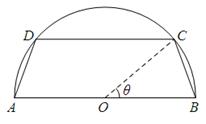
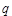 的值,使体积V最大;
的值,使体积V最大;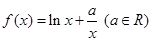
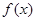 的单调性;
的单调性;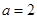 时,求函数
时,求函数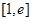 上的最值.
上的最值.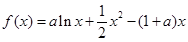 .
.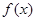 的单调区间;
的单调区间;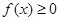 对定义域每的任意
对定义域每的任意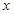 恒成立,求实数
恒成立,求实数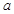 的取值范围;
的取值范围;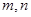 ,不等式
,不等式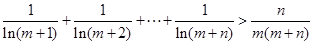 恒成立。
恒成立。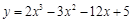 在[0,3]上的最大值和最小值分别是( ).
在[0,3]上的最大值和最小值分别是( ).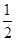 是函数f(x)=ln(x+1)-x+
是函数f(x)=ln(x+1)-x+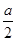 x2的一个极值点。
x2的一个极值点。