题目内容
14.已知{an}是等比数列,Sn是其前n项和,a1,a7,a4成等差数列,求证:2S3,S6,S12-S6成等比数列.分析 通过a1,a7,a4成等差数列可知q3=-$\frac{1}{2}$或q3=1,当q3=1即q=1时显然命题成立;当q3=-$\frac{1}{2}$时,分别计算$\frac{{S}_{6}}{2{S}_{3}}$、$\frac{{S}_{12}-{S}_{6}}{{S}_{6}}$即可.
解答 证明:设该等比数列的公比为q,
∵a1,a7,a4成等差数列,
∴2a7=a1+a4,即2a1q6=a1+a1q3,
∴2q6=1+q3,∴(2q3+1)(q3-1)=0,
解得:q3=-$\frac{1}{2}$或q3=1,
①当q3=1即q=1时,命题显然成立;
②当q3=-$\frac{1}{2}$时,
∵S3=$\frac{{a}_{1}(1-{q}^{3})}{1-q}$,S6=$\frac{{a}_{1}(1-{q}^{6})}{1-q}$,S12=$\frac{{a}_{1}(1-{q}^{12})}{1-q}$,
∴$\frac{{S}_{6}}{2{S}_{3}}$=$\frac{1-{q}^{6}}{2(1-{q}^{3})}$=$\frac{1-(-\frac{1}{2})^{2}}{2[1-(-\frac{1}{2})]}$=$\frac{1}{4}$,
$\frac{{S}_{12}-{S}_{6}}{{S}_{6}}$=$\frac{{q}^{6}-{q}^{12}}{1-{q}^{6}}$=$\frac{(-\frac{1}{2})^{2}-(-\frac{1}{2})^{4}}{1-(-\frac{1}{2})^{2}}$=$\frac{1}{4}$,
∴$\frac{{S}_{6}}{2{S}_{3}}$=$\frac{{S}_{12}-{S}_{6}}{{S}_{6}}$;
综上所述,2S3,S6,S12-S6成等比数列.
点评 本题考查等比数列的性质及判定,注意解题方法的积累,属于中档题.

| A. | -1 | B. | -2 | C. | -3 | D. | 1 |
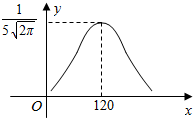 已知随机变量X的概率密度曲线如图所示:
已知随机变量X的概率密度曲线如图所示: