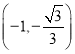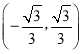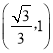题目内容
【题目】已知函数
，下列结论中正确的序号是__________.
①
的图象关于点
中心对称，
②的图象关于
对称，
③
的最大值为
，
④既是奇函数，又是周期函数.
【答案】①②④
【解析】
利用函数图象关于点
对称的充分必要条件：
和函数图象关于直线
对称的充分必要条件：
，结合三角函数的诱导公式和奇偶性，判定①②正确；利用二倍角公式和同角三角函数的关系将
)化为只含有
的表达式，利用换元法并构造函数，使用导数研究单调性，并求得最值，进而判定③错误；利用奇函数的定义和周期函数的定义，结合正余弦函数的周期性可以判定④正确.
,故①正确；
,故②正确；
，其中
.
记
,
,则
,令
，解得
，
列表如下：
-1 |
|
|
|
|
| 1 | |
| - | - | 0 | + | 0 | - | - |
| 0 | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 | 0 |
=
，故
=
，故③错误；
，故
为奇函数，
，故是周期函数，
故④正确.
故答案为：①②④.
练习册系列答案
相关题目
【题目】为改善环境，节约资源，我国自2019年起在全国地级及以上城市全面启动生活垃圾分类，垃圾分类已成为一种潮流.某市一小区的主管部门为了解居民对垃圾分类的认知是否与其受教育程度有关，对该小区居民进行了随机抽样调查，得到如下统计数据的列联表：
知道如何对垃圾进行分类 | 不知道如何对垃圾进行分类 | 合计 | |
未受过高等教育 |
| 10 |
|
受过高等教育 |
|
|
|
合计 |
|
| 50 |
（1）求列联表中的
，
，
，
，
的值，并估计该小区受过高等教育的居民知道如何对垃圾进行分类的概率；
（2）根据列联表判断能否有
的把握认为该小区居民对垃圾分类的认知与其受教育程度有关？
参考数据及公式：
|
|
|
|
|
|
|
|
|
|
|
|
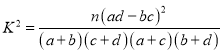，其中
.
