题目内容
19．
已知f（x）是定义在R上的偶函数，当0≤x＜3时，y=x；当x≥3时，$y=-\frac{1}{3}{（x-3）^2}+3$（1）在下面的直角坐标系中直接画出函数f（x）的图象；
（2）根据函数图象写出f（x）的单调区间和值域．
分析 （1）先作出当x≥0时，f（x）的图象，利用偶函数的图象关于y轴对称，再作出当x＜0时，f（x）的图象；
（2）根据（1）中函数的图象，数形结合可得f（x）的单调区间和值域．
解答 解：（1）∵当0≤x＜3时，y=x；当x≥3时，$y=-\frac{1}{3}{（x-3）^2}+3$，
f（x）是定义在R上的偶函数，
故函数f（x）的图象，如图所示：
…6分
（2）函数f（x）的单调递增区间为（-∞，-3]，（0，3），
单调递减区间为（-3，0），[3，+∞）…10分
函数f（x）的值域为（-∞，3]…12分
点评 本题考查的知识点是分段函数的应用，数形结合思想，难度中档．
练习册系列答案
相关题目
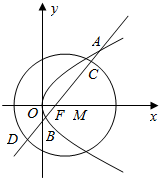如图，抛物线C1：y2=2px（p＞0）和圆C2：（x-1）2+y2=r2（r＞0），M为圆C2的圆心，过抛物线C1的焦点F的直线y=k（x-$\frac{p}{2}$）与C1交于A，B两点，与圆C2交与C，D两点（点C在A，B之间）且△AOF的外心到抛物线C1的准线的距离为$\frac{3}{4}$．
10．x2+y2-x+y+r=0表示一个圆，则r的取值范围是（ ）
| A． | r≤2 | B． | r＜2 | C． | r＜$\frac{1}{2}$ | D． | r≤$\frac{1}{2}$ |
7．函数$f（x）=\frac{1}{{\sqrt{1-x}}}$的定义域是（ ）
| A． | [1，+∞） | B． | （-∞，1） | C． | （-∞，1] | D． | （1，+∞） |