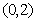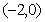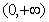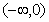题目内容
若函数f(x)=ax3+bx2+cx+d是奇函数,且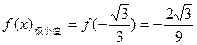
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-1,m](m>-1)上的最大值;
(3)设函数g(x)=,若不等式g(x)·g(2k-x)≥(-k)2在(0,2k)上恒成立,求实数k的取值范围.
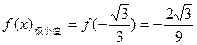
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-1,m](m>-1)上的最大值;
(3)设函数g(x)=,若不等式g(x)·g(2k-x)≥(-k)2在(0,2k)上恒成立,求实数k的取值范围.
f(x)=-x3+x,f(x)max=,(0,)].
解:(1)函数f(x)=ax3+bx2+cx+d是奇函数,则b=d=0,
∴f /(x)=3ax2+c,则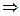
故f(x)=-x3+x;………………………………3分
 (2)∵f /(x)=-3x2+1=-3(x+)(x-)
(2)∵f /(x)=-3x2+1=-3(x+)(x-)
∴f(x)在(-∞,-),(,+∞)上是
增函数,在[-,]上是减函数,
由f(x)=0解得x=±1,x=0,
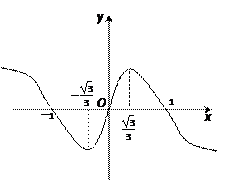
如图所示,
当-1<m<0时,
f(x)max=f(-1)=0;
当0≤m<时,f(x)max=f(m)=-m3+m,
当m≥时,f(x)max=f()=.
故f(x)max=.………………8分
(3)g(x)=(-x),令y=2k-x,则x、y∈R+,且2k=x+y≥2,
又令t=xy,则0<t≤k2,
故函数F(x)=g(x)·g(2k-x)=(-x)(-y)=+xy-
=+xy-=+t+2,t∈(0,k2]
当1-4k2≤0时,F(x)无最小值,不合
当1-4k2>0时,F(x)在(0,]上递减,在[,+∞)上递增,
且F(k2)=(-k)2,∴要F(k2)≥(-k)2恒成立,
必须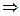 ,
,
故实数k的取值范围是(0,)].………………12分
∴f /(x)=3ax2+c,则
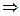
故f(x)=-x3+x;………………………………3分
 (2)∵f /(x)=-3x2+1=-3(x+)(x-)
(2)∵f /(x)=-3x2+1=-3(x+)(x-)∴f(x)在(-∞,-),(,+∞)上是
增函数,在[-,]上是减函数,
由f(x)=0解得x=±1,x=0,
如图所示,
当-1<m<0时,
f(x)max=f(-1)=0;
当0≤m<时,f(x)max=f(m)=-m3+m,
当m≥时,f(x)max=f()=.
故f(x)max=.………………8分
(3)g(x)=(-x),令y=2k-x,则x、y∈R+,且2k=x+y≥2,
又令t=xy,则0<t≤k2,
故函数F(x)=g(x)·g(2k-x)=(-x)(-y)=+xy-
=+xy-=+t+2,t∈(0,k2]
当1-4k2≤0时,F(x)无最小值,不合
当1-4k2>0时,F(x)在(0,]上递减,在[,+∞)上递增,
且F(k2)=(-k)2,∴要F(k2)≥(-k)2恒成立,
必须
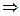 ,
,故实数k的取值范围是(0,)].………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
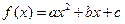 对于
对于 1、
1、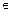 R,且
R,且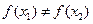 ,求证:方程
,求证:方程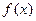 =
=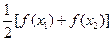 有不等实根,且必有一根属于区间(
有不等实根,且必有一根属于区间(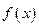 的部分图像如右图所示,则在
的部分图像如右图所示,则在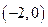 上,下列函数中与
上,下列函数中与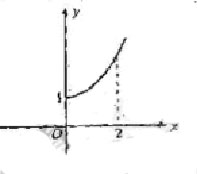
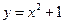
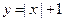

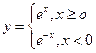
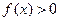 ,则下列一定成立的是( )
,则下列一定成立的是( )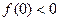
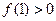
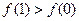
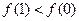
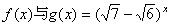 图象关于
图象关于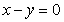 对称,则
对称,则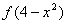 的增区间为( )
的增区间为( )