题目内容
判断y=1-2x3在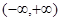 上的单调性,并用定义证明.
上的单调性,并用定义证明.
先设出变量,然后作差,变形定号,下结论来证明单调性。
解析试题分析:证明:任取x1,x2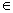 R,且-
R,且-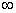 <x1<x2<+
<x1<x2<+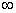 2分
2分
f(x1)-f(x2)
=(1-2x31)-(1-2x32)
=2(x32-x13)
=2(x2-x1)(x22+x1x2+x21)
=2(x2-x1)[(x1+x2)2+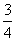 x12] 8分
x12] 8分
∵x2>x1∴x0-x1>0,又(x1+x2)2+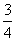 x12>0,
x12>0,
∴f(x1)-f(x2)>0即f(x1)>f(x2) 10分
故f(x)=1-2x3在(-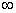 ,+
,+ )上为单调减函数。 12分
)上为单调减函数。 12分
考点:函数单调性
点评:主要是考查了运用定义法来证明函数单调性的运用,属于基础题。

练习册系列答案
相关题目

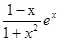 .
.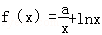 ,g(x)=
,g(x)=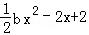 ,a,b∈R.
,a,b∈R.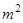 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1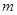 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 
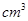 ,高为2
,高为2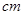 长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?
长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?  .
. 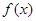 的图像关于点
的图像关于点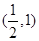 对称;
对称; ,求
,求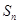 ;
;
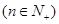 ,
,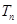 为数列
为数列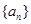 的前
的前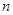 项和,若
项和,若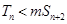 对一切
对一切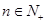 都成立,试求实数
都成立,试求实数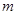 的取值范围.
的取值范围.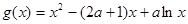
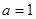 时, 求函数
时, 求函数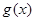 的单调增区间;
的单调增区间;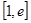 上的最小值;
上的最小值;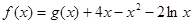 ,
,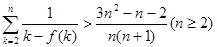 .参考数据:
.参考数据: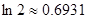 .
.