题目内容
已知函数 .
.
(1)证明函数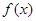 的图像关于点
的图像关于点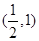 对称;
对称;
(2)若 ,求
,求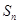 ;
;
(3)在(2)的条件下,若
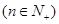 ,
,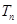 为数列
为数列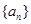 的前
的前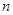 项和,若
项和,若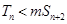 对一切
对一切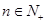 都成立,试求实数
都成立,试求实数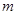 的取值范围.
的取值范围.
(1)函数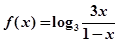 的定义域为
的定义域为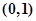 ,设
,设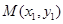 、
、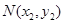 是函数
是函数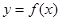 图像上的两点, 其中
图像上的两点, 其中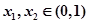 且
且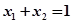 ,则有
,则有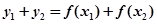
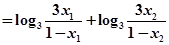
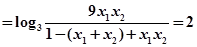 ,因此函数图像关于点
,因此函数图像关于点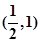 对称(2)
对称(2)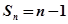 (3)
(3)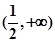
解析试题分析:(1) 证明:因为函数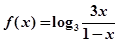 的定义域为
的定义域为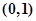 , 设
, 设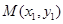 、
、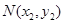 是函数
是函数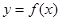 图像上的两点, 其中
图像上的两点, 其中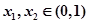 且
且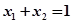 ,
,
则有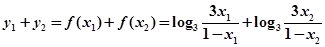
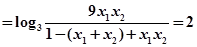
因此函数图像关于点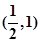 对称 4分
对称 4分
(2)由(1)知当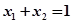 时,
时,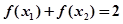
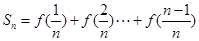 ①
① 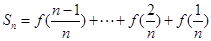 ②
②
①+②得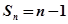 8分
8分
(3)当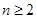 时,
时,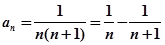
当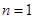 时,
时,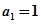 ,
, 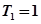
当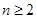 时,
时,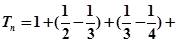
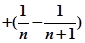 =
= 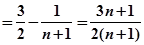
∴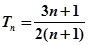 (
(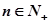 )
)
又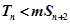 对一切
对一切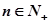 都成立,即
都成立,即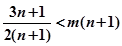 恒成立
恒成立
∴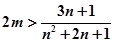 恒成立,又设
恒成立,又设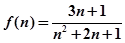 ,
, 所以
所以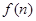 在
在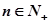 上递减,所以
上递减,所以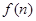 在
在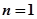 处取得最大值
处取得最大值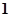
∴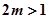 ,即
,即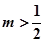
所以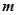 的取值范围是
的取值范围是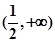 12分
12分
考点:函数对称性,求最值与数列求和
点评:证明函数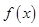 关于点
关于点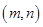 对称只需证明
对称只需证明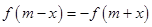 ,第二问数列求和结合通项的特点采用倒序相加法,第三问将不等式恒成立转化为求函数最值,进而可借助于导数求解
,第二问数列求和结合通项的特点采用倒序相加法,第三问将不等式恒成立转化为求函数最值,进而可借助于导数求解

练习册系列答案
相关题目
石家庄市为鼓励居民节约用电,采用分段计费的方法计算电费,每月用电不超过100度时,按每度0.52元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
(1)设月用电 度时,应缴电费
度时,应缴电费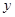 元,写出
元,写出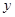 关于
关于 的函数关系式;
的函数关系式;
(2)小明家第一季度缴纳电费情况如下:
| 月份 | 一月 | 二月 | 三月 | 合计 |
| 缴费金额 | 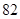 元 元 | 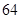 元 元 | 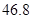 元 元 | 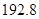 元 元 |
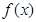 是二次函数,不等式
是二次函数,不等式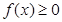 的解集为
的解集为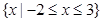 ,且
,且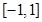 上的最小值是4.
上的最小值是4. ,若对任意的
,若对任意的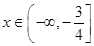 ,
, 均成立,求实数
均成立,求实数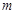 的取值范围.
的取值范围.  万元满足
万元满足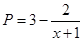 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本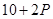 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为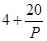 元.
元.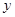 万元表示为促销费用
万元表示为促销费用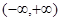 上的单调性,并用定义证明.
上的单调性,并用定义证明. 有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.
有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.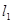 表示神风摩托车厂一天的销售收入与摩托车销售量的关系;
表示神风摩托车厂一天的销售收入与摩托车销售量的关系; 表示摩托车厂一天的销售成本与销售量的关系.
表示摩托车厂一天的销售成本与销售量的关系.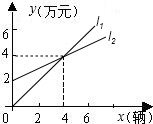
 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得每年改造生态环境总费用的22%。
亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得每年改造生态环境总费用的22%。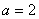 ,
,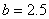 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=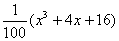 作为生态环境改造投资方案;
作为生态环境改造投资方案;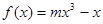 的图象上,以
的图象上,以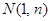 为切点的切线的倾斜角为
为切点的切线的倾斜角为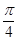 .
.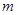 ,
, 的值;
的值;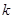 ,使得不等式
,使得不等式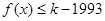 对于
对于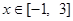 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数 (
(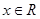 ,
,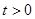 ).
).