题目内容
2．
如图，折线AOB为一条客机的飞机航线，其中OA、OB夹角为$\frac{2π}{3}$，若一架客机沿A-O-B方向飞行至距离O点90km处的C点时，发现航线转折点O处开始产生一个圆形区域的高压气旋，高压气旋范围内的区域为危险区域（含边界），为了保证飞行安全，客机航线需临时调整为CD，若CD与OA的夹角为θ，D在OB上，已知客机的飞行速度为15km/min．（1）当飞机在临时航线上飞行t分钟至点E时，试用t和θ表示飞机到O点的距离OE；
（2）当飞机在临时航线上飞行t分钟时，高压气旋半径r=3t$\sqrt{t}$km，且半径增大到81km时不再继续增大，若CD与OA的夹角θ=$\frac{π}{4}$，试计算飞机在临时航线CD上是否能安全飞行．
分析 （1）OC=90km，AE=15t，∠OCE=θ，在△COE中，由余弦定理取得OE即可．
（2）求出t≤9，代入（1）判断OE与81的大小关系即可．
解答 解：（1）由题意，OC=90km，AE=15t，∠OCE=θ，在△COE中，由余弦定理可得：
∴OE=$\sqrt{8100+225{t}^{2}-2700tcosθ}$；
（2）由题意能安全飞行，必有3t$\sqrt{t}$≤81，可得t≤9，
此时OE=$\sqrt{8100+225×81-2700×9×\frac{\sqrt{2}}{2}}$≈$\sqrt{9145}$＞81，
飞机在临时航线CD上是安全飞行．
点评 本题考查三角函数的几何中的应用，余弦定理的应用，考查计算能力．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
15．设集合S={y|y=3x，x∈R}，T={y|y=x2+1，x∈R}，则S∪T=（ ）
| A． | ∅ | B． | S | C． | T | D． | {0，1} |
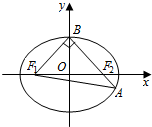如图，在平面直角坐标系xOy中，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点分别为，F1和F2，上顶点为B，BF2，延长线交椭圆于点A，△ABF的周长为8，且$\overrightarrow{B{F_1}}•\overrightarrow{BA}$=0．
如图，已知△ABC的三条高是AD，BE，CF，用向量方法证明：AD，BE，CF相交于一点．