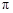题目内容
已知函数 的周期为
的周期为 ,图象的一个对称中心为
,图象的一个对称中心为 ,将函数
,将函数 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个 单位长度后得到函数
单位长度后得到函数 的图象。
的图象。
(Ⅰ)求函数 与
与 的解析式
的解析式
(Ⅱ)是否存在 ,使得
,使得 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定 的个数,若不存在,说明理由;
的个数,若不存在,说明理由;
(Ⅲ)求实数 与正整数
与正整数 ,使得
,使得 在
在 内恰有2013个零点
内恰有2013个零点
 的周期为
的周期为 ,图象的一个对称中心为
,图象的一个对称中心为 ,将函数
,将函数 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个 单位长度后得到函数
单位长度后得到函数 的图象。
的图象。(Ⅰ)求函数
 与
与 的解析式
的解析式(Ⅱ)是否存在
 ,使得
,使得 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定 的个数,若不存在,说明理由;
的个数,若不存在,说明理由;(Ⅲ)求实数
 与正整数
与正整数 ,使得
,使得 在
在 内恰有2013个零点
内恰有2013个零点(Ⅰ)
 (Ⅱ)存在(Ⅲ)当
(Ⅱ)存在(Ⅲ)当 ,
, 时,函数
时,函数 在
在 内恰有
内恰有 个零点
个零点

 (Ⅱ)存在(Ⅲ)当
(Ⅱ)存在(Ⅲ)当 ,
, 时,函数
时,函数 在
在 内恰有
内恰有 个零点
个零点(Ⅰ)由函数 的周期为
的周期为 ,
, ,得
,得
又曲线 的一个对称中心为
的一个对称中心为 ,
,
故 ,得
,得 ,所以
,所以
将函数 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的 倍(纵坐标不变)后可得
倍(纵坐标不变)后可得 的图象,再将
的图象,再将 的图象向右平移
的图象向右平移 个单位长度后得到函数
个单位长度后得到函数
(Ⅱ)当 时,
时, ,
,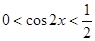
所以
问题转化为方程 在
在 内是否有解
内是否有解
设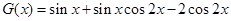 ,
,
则
因为 ,所以
,所以 ,
, 在
在 内单调递增
内单调递增
又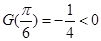 ,
,
且函数 的图象连续不断,故可知函数
的图象连续不断,故可知函数 在
在 内存在唯一零点
内存在唯一零点 ,
,
即存在唯一的 满足题意
满足题意
(Ⅲ)依题意, ,令
,令
当 ,即
,即 时,
时, ,从而
,从而 不是方程
不是方程 的解,所以方程
的解,所以方程 等价于关于
等价于关于 的方程
的方程 ,
,
现研究 时方程解的情况
时方程解的情况
令 ,
,
则问题转化为研究直线 与曲线
与曲线 在
在 的交点情况
的交点情况
 ,令
,令 ,得
,得 或
或
当 变化时,
变化时, 和
和 变化情况如下表
变化情况如下表
当 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
当 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
当 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
当 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
故当 时,直线
时,直线 与曲线
与曲线 在
在 内有无交点,在
内有无交点,在 内有
内有 个交点;
个交点;
当 时,直线
时,直线 与曲线
与曲线 在
在 内有
内有 个交点,在
个交点,在 内无交点;
内无交点;
当 时,直线
时,直线 与曲线
与曲线 在
在 内有
内有 个交点,在
个交点,在 内有
内有 个交点
个交点
由函数 的周期性,可知当
的周期性,可知当 时,直线
时,直线 与曲线
与曲线 在
在 内总有偶数个交点,从而不存在正整数
内总有偶数个交点,从而不存在正整数 ,使得直线
,使得直线 与曲线
与曲线 在
在 内恰有
内恰有 个交点;当
个交点;当 时,直线
时,直线 与曲线
与曲线 在
在 内有
内有 个交点,由周期性,
个交点,由周期性, ,所以
,所以
综上,当 ,
, 时,函数
时,函数 在
在 内恰有
内恰有 个零点
个零点
三角函数解析式的确定相对而言应该比较容易,也就是说即使是20题的第一问往往难度也不会太大,而我们同学可能因为时间的关系而丢掉了捡分的机会,所以建议大家可以先试看看此问是否熟悉,再做整体规划。三角函数的图像变换要千万注意左右平移只对x而言。而第二问对于是否等比的转化是处理的关键,所以函数思想无处不在,要善于运用。第三问从特殊到一般的思想是此问的灵魂,而此法的选择也因为参数分离后三角函数的周期性,所以万物皆有联系,只是平时要练就一双慧眼就不简单了。
【考点定位】 本题考查了三角函数的性质、恒等变换、图像以及函数的零点。将函数的所有性质依托于三角函数展示,并且对多方面能力的综合考查。属于难题,但第一问是送给学生的。
 的周期为
的周期为 ,
, ,得
,得
又曲线
 的一个对称中心为
的一个对称中心为 ,
,
故
 ,得
,得 ,所以
,所以
将函数
 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的 倍(纵坐标不变)后可得
倍(纵坐标不变)后可得 的图象,再将
的图象,再将 的图象向右平移
的图象向右平移 个单位长度后得到函数
个单位长度后得到函数
(Ⅱ)当
 时,
时, ,
,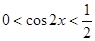
所以

问题转化为方程
 在
在 内是否有解
内是否有解设
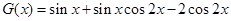 ,
,
则

因为
 ,所以
,所以 ,
, 在
在 内单调递增
内单调递增又
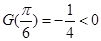 ,
,
且函数
 的图象连续不断,故可知函数
的图象连续不断,故可知函数 在
在 内存在唯一零点
内存在唯一零点 ,
,即存在唯一的
 满足题意
满足题意(Ⅲ)依题意,
 ,令
,令
当
 ,即
,即 时,
时, ,从而
,从而 不是方程
不是方程 的解,所以方程
的解,所以方程 等价于关于
等价于关于 的方程
的方程 ,
,
现研究
 时方程解的情况
时方程解的情况令
 ,
,
则问题转化为研究直线
 与曲线
与曲线 在
在 的交点情况
的交点情况 ,令
,令 ,得
,得 或
或
当
 变化时,
变化时, 和
和 变化情况如下表
变化情况如下表 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  | 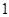 |  |  |  |  |
 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
当
 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
当
 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
当
 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
故当
 时,直线
时,直线 与曲线
与曲线 在
在 内有无交点,在
内有无交点,在 内有
内有 个交点;
个交点;当
 时,直线
时,直线 与曲线
与曲线 在
在 内有
内有 个交点,在
个交点,在 内无交点;
内无交点;当
 时,直线
时,直线 与曲线
与曲线 在
在 内有
内有 个交点,在
个交点,在 内有
内有 个交点
个交点由函数
 的周期性,可知当
的周期性,可知当 时,直线
时,直线 与曲线
与曲线 在
在 内总有偶数个交点,从而不存在正整数
内总有偶数个交点,从而不存在正整数 ,使得直线
,使得直线 与曲线
与曲线 在
在 内恰有
内恰有 个交点;当
个交点;当 时,直线
时,直线 与曲线
与曲线 在
在 内有
内有 个交点,由周期性,
个交点,由周期性, ,所以
,所以
综上,当
 ,
, 时,函数
时,函数 在
在 内恰有
内恰有 个零点
个零点三角函数解析式的确定相对而言应该比较容易,也就是说即使是20题的第一问往往难度也不会太大,而我们同学可能因为时间的关系而丢掉了捡分的机会,所以建议大家可以先试看看此问是否熟悉,再做整体规划。三角函数的图像变换要千万注意左右平移只对x而言。而第二问对于是否等比的转化是处理的关键,所以函数思想无处不在,要善于运用。第三问从特殊到一般的思想是此问的灵魂,而此法的选择也因为参数分离后三角函数的周期性,所以万物皆有联系,只是平时要练就一双慧眼就不简单了。
【考点定位】 本题考查了三角函数的性质、恒等变换、图像以及函数的零点。将函数的所有性质依托于三角函数展示,并且对多方面能力的综合考查。属于难题,但第一问是送给学生的。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
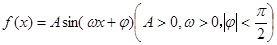 的一段图象如图所示.
的一段图象如图所示.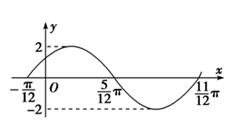
 的解析式;
的解析式; 个单位,得到
个单位,得到 的图象,求直线
的图象,求直线 与函数
与函数 的图象在
的图象在 内所有交点的坐标.
内所有交点的坐标. ,下面结论错误的是( )
,下面结论错误的是( ) 的最小正周期为
的最小正周期为
 上是增函数
上是增函数 对称
对称 在区间
在区间 上的最小值是( )
上的最小值是( )


 )sin(
)sin( )的单调递增区间为( )
)的单调递增区间为( )  )π,(k+1)π]
)π,(k+1)π] ,
, ,且
,且 ,
, ,则
,则 的值是( )
的值是( ) 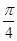



 ,给出下列命题:
,给出下列命题: 的图象关于直线
的图象关于直线 对称;②函数
对称;②函数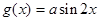 的图象向左平移
的图象向左平移 个单位而得到;③把函数
个单位而得到;③把函数 的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的
的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的 倍,可以得到函数
倍,可以得到函数 )的图象;④若函数
)的图象;④若函数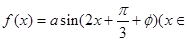 R)为偶函数,则
R)为偶函数,则 .其中正确命题的序号有 ;(把你认为正确的命题的序号都填上)。
.其中正确命题的序号有 ;(把你认为正确的命题的序号都填上)。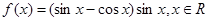 ,则
,则 的最小正周期是 。
的最小正周期是 。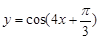 图象的两条相邻对称轴间的距离为
图象的两条相邻对称轴间的距离为