题目内容
【题目】已知函数![]() ,
,
(1)若对任意![]() ,
,![]() 且
且![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)在第(1)问求出的实数![]() 的范围内,若存在一个与
的范围内,若存在一个与![]() 有关的负数
有关的负数![]() ,使得对任意
,使得对任意![]() 时
时![]() 恒成立,求
恒成立,求![]() 的最小值及相应的
的最小值及相应的![]() 值.
值.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)利用作差法比较大小即可;
(2)由(1)可知![]() 的图象是开口向上,对称轴
的图象是开口向上,对称轴![]() 的抛物线,将对任意
的抛物线,将对任意![]() 时
时![]() 恒成立转化为
恒成立转化为![]() 且
且![]() ,分别讨论
,分别讨论![]() 和
和![]() 的情况,进而求解即可
的情况,进而求解即可
(1)依题意知![]()
![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,则
,则![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]()
(2)对任意![]() 时,“
时,“![]() 恒成立”等价于“
恒成立”等价于“![]() 且
且![]() ”,
”,
由(1)可知实数![]() 的取值范围是
的取值范围是![]() ,
,
故![]() 的图象是开口向上,对称轴
的图象是开口向上,对称轴![]() 的抛物线,
的抛物线,
①当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,
上单调递增,
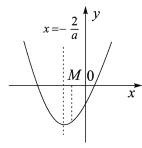
∴![]() ,
,![]() ,则
,则![]() ,
,
要使![]() 最小,只需要
最小,只需要![]() ,
,
若![]() 即
即![]() 时,无解;若
时,无解;若![]() 即
即![]() 时,
时,
解得![]() (舍去)或
(舍去)或![]()
故![]() (当且仅当
(当且仅当![]() 时取等号);
时取等号);
②当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 递增,
递增,
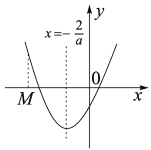
![]() ,
,![]() ,则
,则![]() ,
,
要使![]() 最小,则
最小,则![]() ,即
,即![]() ,
,
解得![]() (舍去)或
(舍去)或![]() (当且仅当
(当且仅当![]() 时取等号)
时取等号)
综上所述,当![]() 时,
时,![]() 的最小值为
的最小值为![]()

练习册系列答案
相关题目