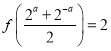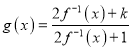题目内容
【题目】设
为三次函数，且其图象关于原点对称，当
时，
的极小值为-1，则
（1）函数的解析式
__________；
（2）函数的单调递增区间为___________。
【答案】（1）
（2）
和
【解析】
（1）先利用待定系数法设出f（x）的解析式，再根据奇偶性以及极值建立等式关系，求出参数即可；
（2）利用导数研究函数的单调性，求出函数
的单调递增
（1）设f（x）=ax3+bx2+cx+d（a≠0）
∵其图象关于原点对称，即f（-x）=-f（x）
得-ax3+bx2-cx+d=-ax3-bx2-cx-d
∴b=d=0，
则有f（x）=ax3+cx
由f′（x）=3ax2+c，依题意得
∴
由①②得a=4，c=-3故所求的解析式为：f（x）=4x3-3x．
（2）由（1）可得f（x）=4x3-3x．则令f′（x）=12x2-3＞0
解得：
或
，即函数的单调递增区间为和.
即答案为(1). (2). 和.
练习册系列答案
相关题目
