题目内容
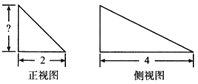
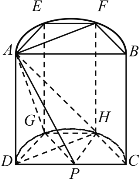
【题目】如图，在长方形ABCD中，AB=
,AD=2,E,F为线段AB的三等分点，G、H为线段DC的三等分点．将长方形ABCD卷成以AD为母线的圆柱W的半个侧面，AB、CD分别为圆柱W上、下底面的直径．
（Ⅰ）证明：平面ADHF⊥平面BCHF；
（Ⅱ）若P为DC的中点，求三棱锥H—AGP的体积．
【答案】（1）见解析（2）
【解析】
(1)
在下底面圆周上，且
为下底面半圆的直径,得到DH垂直于HC，
进而得到
平面
，最终根据面面垂直的判定定理得到面面垂直；(2) 三棱锥
的体积
，因为
为
的三等分点结合题干条件得到
均为边长等于
的等边三角形，进而求得结果.
（1）因为在下底面圆周上，且为下底面半圆的直径
所以
又因为，且
，所以平面
又因为
平面
，所以平面
平面
（2）设下底面半径为
，
由题
，所以
，
因为下底面半圆圆心为
，
所以
又因为为的三等分点，
所以均为边
长等于的等边三角形，
所以
的面积
所以三棱锥的体积
练习册系列答案
阅读快车系列答案
相关题目
【题目】某地区某农产品近几年的产量统计如表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
（Ⅰ）根据表中数据，建立
关于的线性回归方程
；
（Ⅱ）根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据
，其回归直线的斜率和截距的最小二乘估计分别为：
，
.(参考数据:
，计算结果保留小数点后两位）
