题目内容
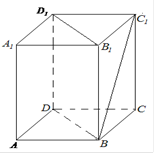
)如图,在正三棱柱ABC—A1B1C1中,AB=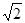 AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。
AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。
(1)证明B1F//平面ADE;
(2)证明平面ABC1⊥平面C1DF;
(3)求直线AD和平面ABC1所成角的正弦值。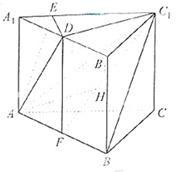
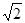 AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。
AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。(1)证明B1F//平面ADE;
(2)证明平面ABC1⊥平面C1DF;
(3)求直线AD和平面ABC1所成角的正弦值。

(1)略 (2)略 (3)

(I)关键证明:B1F//AD.
(2)证明:AB 平面C
平面C DF.
DF.
(3) 过点D作DH垂直C F于点H,则DH
F于点H,则DH 平面ABC
平面ABC .连接AH,则
.连接AH,则 HAD是AD和平面ABC
HAD是AD和平面ABC 所成的角,是解题的关键。
所成的角,是解题的关键。
(1)证明: 如图所示,在正三棱柱 中, D是
中, D是 的中点,点F是AB的中点,所以
的中点,点F是AB的中点,所以 ,且
,且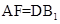 ,所以四边形
,所以四边形 是平行四边形,所以
是平行四边形,所以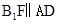 , AD在平面ADE内,
, AD在平面ADE内,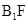 不在平面ADE内, 故
不在平面ADE内, 故 . (4分)
. (4分)
(2)证明:如图所示,F是AB的中点,连接DF、DC、CF,由正三棱柱ABC- A B
B C
C 的性质及D是A
的性质及D是A B的中点知
B的中点知 ,
, ,又C
,又C D
D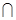 DF=D,所以A
DF=D,所以A B
B
 平面C
平面C DF,而AB∥A
DF,而AB∥A B
B ,所以AB
,所以AB 平面C
平面C DF,又AB
DF,又AB 平面ABC
平面ABC ,故平面AB C
,故平面AB C
 平面C
平面C DF。
DF。
(3)解: 过点D作DH垂直C F于点H,则DH
F于点H,则DH 平面ABC
平面ABC .连接AH,则
.连接AH,则 HAD是AD和平面ABC
HAD是AD和平面ABC 所成的角。由已知AB=
所成的角。由已知AB=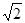 A A
A A ,不妨设
,不妨设
A A =
=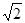 ,则AB=2,DF=
,则AB=2,DF=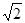 ,D C
,D C =
= ,C
,C F=
F= ,AD=
,AD=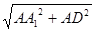 =
= ,DH=
,DH=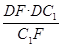 =
= —
— ,所以 sin
,所以 sin HAD=
HAD= =
= 。即直线AD和平面AB C
。即直线AD和平面AB C 所成角的正弦值为
所成角的正弦值为 。
。
(2)证明:AB
 平面C
平面C DF.
DF.(3) 过点D作DH垂直C
 F于点H,则DH
F于点H,则DH 平面ABC
平面ABC .连接AH,则
.连接AH,则 HAD是AD和平面ABC
HAD是AD和平面ABC 所成的角,是解题的关键。
所成的角,是解题的关键。(1)证明: 如图所示,在正三棱柱
 中, D是
中, D是 的中点,点F是AB的中点,所以
的中点,点F是AB的中点,所以 ,且
,且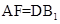 ,所以四边形
,所以四边形 是平行四边形,所以
是平行四边形,所以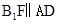 , AD在平面ADE内,
, AD在平面ADE内,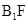 不在平面ADE内, 故
不在平面ADE内, 故 . (4分)
. (4分) (2)证明:如图所示,F是AB的中点,连接DF、DC、CF,由正三棱柱ABC- A
 B
B C
C 的性质及D是A
的性质及D是A B的中点知
B的中点知 ,
, ,又C
,又C D
D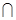 DF=D,所以A
DF=D,所以A B
B
 平面C
平面C DF,而AB∥A
DF,而AB∥A B
B ,所以AB
,所以AB 平面C
平面C DF,又AB
DF,又AB 平面ABC
平面ABC ,故平面AB C
,故平面AB C
 平面C
平面C DF。
DF。 (3)解: 过点D作DH垂直C
 F于点H,则DH
F于点H,则DH 平面ABC
平面ABC .连接AH,则
.连接AH,则 HAD是AD和平面ABC
HAD是AD和平面ABC 所成的角。由已知AB=
所成的角。由已知AB=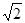 A A
A A ,不妨设
,不妨设A A
 =
=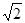 ,则AB=2,DF=
,则AB=2,DF=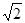 ,D C
,D C =
= ,C
,C F=
F= ,AD=
,AD=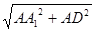 =
= ,DH=
,DH=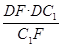 =
= —
— ,所以 sin
,所以 sin HAD=
HAD= =
= 。即直线AD和平面AB C
。即直线AD和平面AB C 所成角的正弦值为
所成角的正弦值为 。
。
练习册系列答案
相关题目
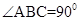 ,
,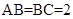 ,二面角P-AB-C为
,二面角P-AB-C为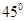 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.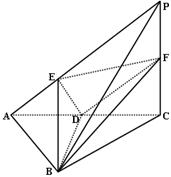




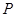 是正四面体
是正四面体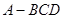 的棱
的棱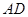 中点,则直线
中点,则直线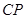 与平面
与平面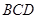 所成角的正弦值为__________.
所成角的正弦值为__________.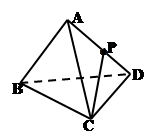
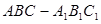 中,
中, 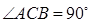 ,
,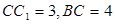 ,
, 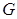 是
是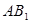 和
和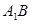 的交点, 若
的交点, 若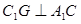 .
. 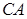 的长; (2)求点
的长; (2)求点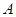 到平面
到平面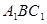 的距离;
的距离;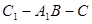 的平面角的正弦值的大小.
的平面角的正弦值的大小.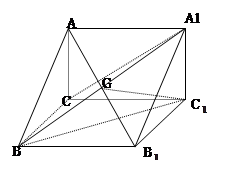
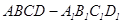 中,
中,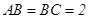 ,
,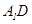 与
与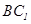
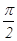 ,则
,则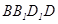 所成角的正弦值为( )
所成角的正弦值为( )







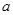 的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,
的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,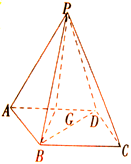
 中,
中, 为顶点在底面上的射影,且
为顶点在底面上的射影,且 ,则直线
,则直线 与平面
与平面 所成角的大小等于
所成角的大小等于