题目内容
已知三棱锥P—ABC中,PC⊥底面ABC,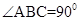 ,
,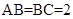 ,二面角P-AB-C为
,二面角P-AB-C为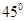 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.
(Ⅰ)求证:AP⊥平面BDE;
(Ⅱ)求直线EB与平面PAC所成的角。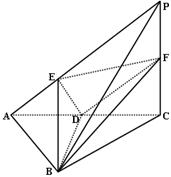
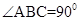 ,
,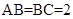 ,二面角P-AB-C为
,二面角P-AB-C为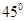 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.(Ⅰ)求证:AP⊥平面BDE;
(Ⅱ)求直线EB与平面PAC所成的角。

(1)见解析;(2)
(1)证明 PC⊥底面ABC
PC⊥底面ABC ,又AB=BC,D为AC中点
,又AB=BC,D为AC中点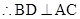
 平面ACP
平面ACP 平面ACP
平面ACP ,又
,又 平面BDE
平面BDE
(2)由(1)的证明知 平面ACP
平面ACP 为直线EB与平面PAC所成的角。
为直线EB与平面PAC所成的角。
 为PB在平面ABC上的射影
为PB在平面ABC上的射影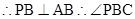 为二面角P-AB-C的平面角
为二面角P-AB-C的平面角



(1)证明
 PC⊥底面ABC
PC⊥底面ABC ,又AB=BC,D为AC中点
,又AB=BC,D为AC中点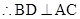
 平面ACP
平面ACP 平面ACP
平面ACP ,又
,又 平面BDE
平面BDE(2)由(1)的证明知
 平面ACP
平面ACP 为直线EB与平面PAC所成的角。
为直线EB与平面PAC所成的角。 为PB在平面ABC上的射影
为PB在平面ABC上的射影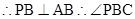 为二面角P-AB-C的平面角
为二面角P-AB-C的平面角


本试题主要考查了线面的垂直问题以及线面角的求解的综合运用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
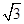 ,D、E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为 ( )
,D、E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为 ( )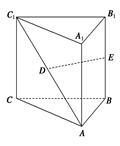
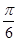 B.
B.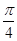 C.
C.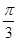 D.
D.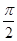
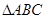 为正三角形,
为正三角形,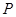 是
是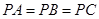 且
且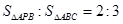 ,则二面角
,则二面角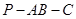 的大小___________;
的大小___________; 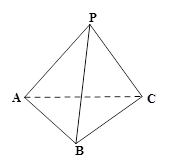
 -
- 中,
中, 与平面
与平面 所成角的余弦值为
所成角的余弦值为 .
. .
. .
. .
.

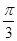
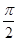
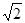 AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。
AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。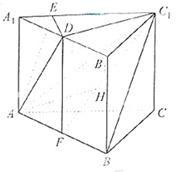
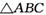 的外接圆为球O的小圆
的外接圆为球O的小圆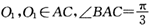 ,AB=1,PA=2.则下列结论正确的是
,AB=1,PA=2.则下列结论正确的是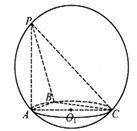

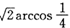
 ,
, 与底面成30°角。
与底面成30°角。 为垂足,求证:
为垂足,求证: ;
;
 的棱长是3,点
的棱长是3,点 分别是棱
分别是棱 的中点,则异面直线MN与
的中点,则异面直线MN与 所成的角是 .
所成的角是 .