题目内容
本小题满分12分）
设函数
在
及
时取得极值．
（Ⅰ）求a、b的值(6分)；
（Ⅱ）若对于任意的
，都有
成立，求c的取值范围(6分)
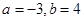（2）
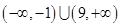
解析
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
鸿图图书寒假作业假期作业吉林大学出版社系列答案题目内容
本小题满分12分）
设函数在及时取得极值．
（Ⅰ）求a、b的值(6分)；
（Ⅱ）若对于任意的，都有成立，求c的取值范围(6分)
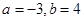（2）
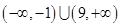
解析
鸿图图书寒假作业假期作业吉林大学出版社系列答案
，
在
处与直线
相切；
的值；②求函数
上的最大值;
时，若不等式
对所有的
都成立，求实数
的取值范围.
．
时，求
的极值；
时，试比较
的大小；
（
）．
.
在
上是增函数，求实数
的取值范围；
是
上的最小值和最大值.
在点
处取得极值
。
的值；
有极大值28，求
上的最小值。
（万元）与处理量
（吨）之间的函数关系可近似地表示为：
， 且每处理一吨二氧化碳可得价值为
万元的某种化工产品. 
时，判断该技术改进能否获利？如果能获利，求出最大利润；如果不能获利，则国家至少需要补贴多少万元，该工厂才不亏损？ 
x2＋lnx.
x3.
。
，函数
在
上既能取到极大值，又能取到极小值，求
的取值范围；
时，
对任意的
恒成立，求
的取值范围；
在
上为单调递增函数.
的取值范围；
，
，求
的最小值．