题目内容
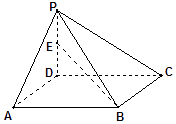
【题目】长方体ABCD－A1B1C1D1中，AB＝BC＝2，D1D＝3，点M是B1C1的中点，点N是AB的中点．建立如图所示的空间直角坐标系.
（1）写出点D、N、M的坐标；
（2）求线段MD、MN的长度．
【答案】
（1）解:因为D是原点，则D(0,0,0)．
由AB＝BC＝2，D1D＝3，
得A(2,0,0)、B(2,2,0)、C(0,2,0)、B1(2,2,3)、C1(0,2,3)．
∵N是AB的中点，∴N(2,1,0)．
同理可得M(1,2,3)．
（2）解:由两点间距离公式，得
|MD|＝ 
＝ 
，
|MN|＝ 
.
【解析】（1）根据所建立的空间直角坐标系及所给点的特征很容易写出各点的坐标；（2）利用空间直角坐标系中两点之间的距离公式求线段MD，MN的长度即可.
练习册系列答案
相关题目
