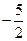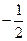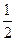题目内容
已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
| A.n(2n-1) | B.(n+1)2 |
| C.n2 | D.(n-1)2 |
C
分析:由题意,等比数列{an}a>0,n=1,2,…,且a5?a2n-5=22n(n≥3),又当n>1时,log2a1+log2a3+log2a5+…+log2a2n-1=log2a1a3a5…a2n-1.由等比数列的性质m+n=s+t,aman=asat.求出a1a3a5…a2n-1的值,即可求出正确答案,得出正确选项
解:由题意等比数列{an}a>0,n=1,2,…,
当n>1时,log2a1+log2a3+log2a5+…+log2a2n-1=log2a1a3a5…a2n-1.
又a5?a2n-5=22n(n≥3)
∴a1a3a5…a2n-1=(2n)n=2n 2
∴log2a1+log2a3+log2a5+…+log2a2n-1=log22n 2=n2
故选C

练习册系列答案
相关题目
 中,
中,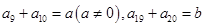 ,则
,则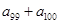 等于
等于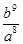 B.
B. 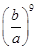 C.
C. 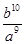 D
D 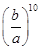
 中,
中, =0,且对任意k
=0,且对任意k ,
, 成等差数列,
成等差数列, 成等比数列;
成等比数列; 的通项公式;
的通项公式; 的前
的前 项和为
项和为 ,且
,且
 ,
, 及
及 ;(2)证明:数列
;(2)证明:数列 .
.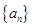 ,
,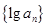 成等差数列,公差
成等差数列,公差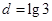 ,且
,且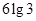 ,则
,则

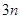

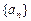 中,
中,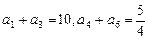 ,则
,则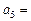 ________________
________________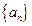 满足
满足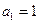 ,
,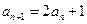 ,若数列
,若数列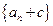 恰为等比数列,则
恰为等比数列,则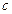 的值为 .
的值为 .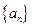 中,
中,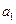 和
和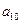 是方程
是方程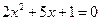 的两个根,则
的两个根,则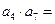 ( )
( )