题目内容
(本题9分)函数
(Ⅰ)判断并证明 的奇偶性;
的奇偶性;
(Ⅱ)求证:在定义域内 恒为正。
恒为正。
(Ⅰ) 是偶函数。(Ⅱ)根据奇偶性,只需证明
是偶函数。(Ⅱ)根据奇偶性,只需证明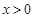 时,函数
时,函数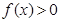 。
。
解析试题分析:(Ⅰ)判断: 是偶函数。 1分
是偶函数。 1分
证明: 的定义域为
的定义域为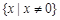 关于原点对称 1分
关于原点对称 1分
对于任意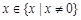
有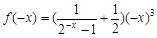
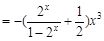
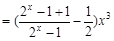
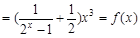 ,所以
,所以 是偶函数。 3分
是偶函数。 3分
(Ⅱ)当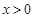 时,
时,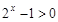 且
且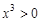 ,所以
,所以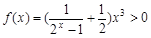 2分
2分
又因为 是偶函数,
是偶函数,
所以当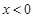 时,
时,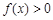 也成立。 2分
也成立。 2分
综上,在定义域内 恒为正。
恒为正。
考点:函数的性质:奇偶性。
点评:判断一个函数的奇偶性有两步:①求函数的定义域,判断函数的定义域关于原点对称;②判断 与
与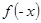 的关系。尤其是做大题时不要忘记求函数的定义域。
的关系。尤其是做大题时不要忘记求函数的定义域。

练习册系列答案
相关题目
 (
( ).
). 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值; ,
,
 ,总有
,总有 ,求实数
,求实数 ,其中常数a > 0.
,其中常数a > 0. 上是减函数;
上是减函数; 和
和 组成数对(
组成数对( ,并构成函数
,并构成函数
 ,且
,且 的概率;
的概率; 在区间[
在区间[ 上是增函数的概率.
上是增函数的概率. 处取得极值2。
处取得极值2。 求函数
求函数 的表达式;
的表达式; 满足什么条件时,函数
满足什么条件时,函数 上单调递增?
上单调递增? 为
为 图象上任意一点,直线与
图象上任意一点,直线与 的取值范围
的取值范围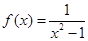 .
. 的定义域为A,求集合A;
的定义域为A,求集合A;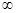 )上单调性,并用定义加以证明.
)上单调性,并用定义加以证明. 上的函数
上的函数 ,对于任意的实数
,对于任意的实数 ,恒有
,恒有 ,且当
,且当 时,
时, 。
。 及
及 的值域。
的值域。 ,
, ,
, ,求
,求 的范围。
的范围。 为奇函数,
为奇函数,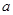 为常数,
为常数, 在区间
在区间 上单调递增;
上单调递增; 上的每一个
上的每一个 值,不等式
值,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.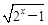 (a>0,a≠1).
(a>0,a≠1).