题目内容
10.设函数f(x)=a2x2(a>0),g(x)=blnx.(1)若函数y=f(x)图象上的点到直线x-y-3=0距离的最小值为2$\sqrt{2}$,求a的值;
(2)对于函数f(x)与g(x)定义域上的任意实数x,若存在常数k,m,使得f(x)≥kx+m和g(x)≤kx+m都成立,则称直线y=kx+m为函数f(x)与g(x)的“分界线”.设a=$\frac{\sqrt{2}}{2}$,b=e,试探究f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
分析 (1)直接运用点到直线的距离公式,然后求解即可得到答案.
(2)属于新定义的题目,可以用函数求导数求最值的方法解答.
解答 解:(1)因为f(x)=a2x2,所以f′(x)=2a2x,
令f′(x)=2a2x=1
得:x=$\frac{1}{2{a}^{2}}$,
此时y=$\frac{1}{4{a}^{2}}$,
则点($\frac{1}{2{a}^{2}}$,$\frac{1}{4{a}^{2}}$)到直线x-y-3=0的距离为2$\sqrt{2}$,
即$\frac{|\frac{1}{2{a}^{2}}-\frac{1}{4{a}^{2}}-3|}{\sqrt{2}}$=2$\sqrt{2}$,
解之得a=$\frac{\sqrt{7}}{14}$;
(2)设F(x)=f(x)-g(x)=$\frac{1}{2}$x2-elnx,
则F′(x)=x-$\frac{e}{x}$,
所以当0<x<$\sqrt{e}$时,F′(x)<0;当x>$\sqrt{e}$时,F′(x)>0.
因此x=$\sqrt{e}$时,F(x)取得最小值0,
则f(x)与g(x)的图象在x=$\sqrt{e}$处有公共点($\sqrt{e}$,$\frac{1}{2}$e).
设f(x)与g(x)存在“分界线”,
方程为y-$\frac{1}{2}$e=k(x-$\sqrt{e}$),即y=kx+$\frac{1}{2}$e-k$\sqrt{e}$,
由f(x)≥kx+$\frac{1}{2}$e-k$\sqrt{e}$在x∈R恒成立,
则x2-2kx-e+2k$\sqrt{e}$≥0在x∈R恒成立.
所以△=4k2-4(2k$\sqrt{e}$-e)=4k2-8k$\sqrt{e}$+4e=4(k-$\sqrt{e}$)2≤0成立,
因此k=$\sqrt{e}$.
下面证明g(x)≤$\sqrt{e}$x-$\frac{1}{2}$e(x>0)恒成立.
设G(x)=elnx-x$\sqrt{e}$+$\frac{1}{2}$e(x>0),
则G′(x)=$\frac{e}{x}$-$\sqrt{e}$=$\frac{\sqrt{e}(\sqrt{e}-x)}{x}$.
所以当0<x<$\sqrt{e}$时,G′(x)>0;当x>$\sqrt{e}$时,G′(x)<0.
因此x=$\sqrt{e}$时G(x)取得最大值0,则g(x)≤$\sqrt{e}$x-$\frac{1}{2}$e成立.
故所求“分界线”方程为:y=$\sqrt{e}$x-$\frac{1}{2}$e.
点评 此题主要考查点到直线距离公式的应用及利用导函数求闭区间极值问题,题中涉及到新定义的问题,此类型的题目需要仔细分析再求解,综合性较强,有一定的技巧性,属于难题.

| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
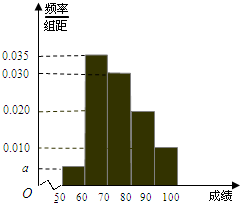 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:| 组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均数.
| A. | cos(2x-1) | B. | -2cos(2x-1) | C. | 2cos(2x-1) | D. | -cos(2x-1) |