题目内容
【题目】.(本小题满分16分)
已知函数![]() ,并设
,并设![]() ,
,
(1)若![]() 图像在
图像在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 、
、![]() 的值;
的值;
(2)若函数![]() 是
是![]() 上单调递减,则
上单调递减,则
① 当![]() 时,试判断
时,试判断![]() 与
与![]() 的大小关系,并证明之;
的大小关系,并证明之;
② 对满足题设条件的任意![]() 、
、![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围
的取值范围
【答案】(1)因为![]() ,所以
,所以![]() , …………………2分
, …………………2分
又因为![]() 图像在
图像在![]() 处的切线方程为
处的切线方程为![]() ,
,
所以 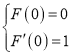 ,即
,即![]() ,解得
,解得 ![]() ,
,![]() . ……………………………………4分
. ……………………………………4分
(2)①因为![]() 是
是![]() 上的单调递减函数,所以
上的单调递减函数,所以![]() 恒成立,
恒成立,
即![]() 对任意的
对任意的![]() 恒成立, ………………………………………6分
恒成立, ………………………………………6分
所以![]() ,所以
,所以![]() ,即
,即![]() 且
且![]() ,
,
令![]() ,由
,由![]() ,知
,知![]() 是减函数,
是减函数,
故![]() 在
在![]() 内取得最小值
内取得最小值![]() ,又
,又![]() ,
,
所以![]() 时,
时,![]() . ……………………………………10分
. ……………………………………10分
② 由①知,![]() ,当
,当![]() 时,
时,![]() 或
或![]() ,
,
因为![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() 或
或![]() ,所以
,所以![]() ,
,
而![]() ,
,
所以![]() 或
或![]() ,
,
不等式![]() 等价于
等价于![]() ,
,
变为![]() 或
或![]() 恒成立,
恒成立,![]() , ………………………………………………12分
, ………………………………………………12分
当![]() 时,
时,![]() ,即
,即![]() ,所以不等式
,所以不等式![]() 恒成立等价于
恒成立等价于![]() 恒成立,等价于
恒成立,等价于![]() , ………………………………………14分
, ………………………………………14分
而 ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以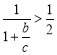 ,
,
所以![]() ,所以
,所以![]() . ……………………………………………………16分
. ……………………………………………………16分
【解析】略

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
【题目】2019年,中华人民共和国成立70周年,为了庆祝建国70周年,某中学在全校进行了一次爱国主义知识竞赛,共1000名学生参加,答对题数(共60题)分布如下表所示:
组别 |
|
|
|
|
|
|
频数 | 10 | 185 | 265 | 400 | 115 | 25 |
答对题数![]() 近似服从正态分布
近似服从正态分布![]() ,
,![]() 为这1000人答对题数的平均值(同一组数据用该组区间的中点值作为代表).
为这1000人答对题数的平均值(同一组数据用该组区间的中点值作为代表).
(1)估计答对题数在![]() 内的人数(精确到整数位).
内的人数(精确到整数位).
(2)学校为此次参加竞赛的学生制定如下奖励方案:每名同学可以获得2次抽奖机会,每次抽奖所得奖品的价值与对应的概率如下表所示.
获得奖品的价值(单位:元) | 0 | 10 | 20 |
概率 |
|
|
|
用![]() (单位:元)表示学生甲参与抽奖所得奖品的价值,求
(单位:元)表示学生甲参与抽奖所得奖品的价值,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.