Question

【题目】设动点到定点的距离比它到轴的距离大，记点的轨迹为曲线.

（1）求点的轨迹方程；

（2）若圆心在曲线上的动圆过点，试证明圆与轴必相交，且截轴所得的弦长为定值.

Answer 1

【答案】(1) ；(2)证明见解析.

【解析】试题分析：

（1）由题意可得曲线为抛物线，根据抛物线的定义可得其方程．（2）结合题意设出圆心的坐标，并根据圆过点A得到圆的标准方程，在圆方程中令后可得关于x的二次方程，根据此方程判别式可判断圆与x轴相交，同时并根据数轴上两点间的距离求出弦长．

试题解析：

（1）依题意知，动点到定点 的距离等于到直线的距离，

∴曲线是以原点为顶点， 为焦点的抛物线．

设曲线C的方程为,

则，

∴，

∴曲线方程是 ．

（2）

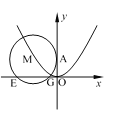
设圆心为，则，

∵圆过 ，

∴圆的方程为，

令得．

∵

∴圆与轴必相交，

设圆M与轴的两交点分别为E ，G

则， ，　

∴ ，

∴=4．

故圆截轴所得的弦长为定值．