题目内容
已知正四棱锥P-ABCD的高为4
,侧棱与底面所成的角为60°,则该正四棱锥的侧面积是
| 3 |
32
| 7 |
32
.| 7 |
分析:先求四棱锥的底面边长,再求棱锥的斜高,然后求出表面积.
解答:解: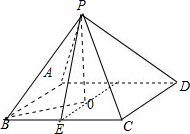 设底面边长为a.在直角三角形POB中,BO=POcot∠PBO=4
设底面边长为a.在直角三角形POB中,BO=POcot∠PBO=4
×cot60°=4=
a,∴a=4
OE=
=2
.斜高PE=
=2
.正四棱锥的侧面积等于
×c×PE=
×16
×2
=32
.
故答案为:32
.
 设底面边长为a.在直角三角形POB中,BO=POcot∠PBO=4
设底面边长为a.在直角三角形POB中,BO=POcot∠PBO=4| 3 |
| ||
| 2 |
| 2 |
OE=
| a |
| 2 |
| 2 |
| PO2+OE2 |
| 14 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 14 |
| 7 |
故答案为:32
| 7 |
点评:本题考查正四棱锥的结构特征、侧面积的计算.准确利用高、底边、斜高的数量关系是关键.

练习册系列答案
相关题目
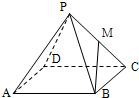
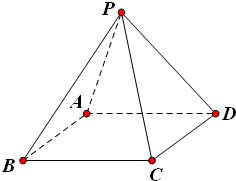 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h. ,M是侧棱PC的中点,则异面直线PA与BM所成角为 .
,M是侧棱PC的中点,则异面直线PA与BM所成角为 .