题目内容
 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
(1)用h表示底面边长,并求正四棱锥体积V的最大值;
(2)当V取最大值时,求异面直线AB和PD所成角的大小.
(结果用反三角函数值表示)
 解:(1)设底面边长为a,斜高为H,由题意a2+2aH=2,所以
解:(1)设底面边长为a,斜高为H,由题意a2+2aH=2,所以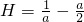 ,(2分)
,(2分)又因为
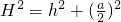 ,所以
,所以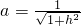 (4分)
(4分)因而
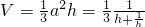 ,
,当且仅当h=1时,体积最大,
 .(8分)
.(8分)此时
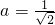 ,
,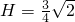 .
.(2)∠PDQ即为异面直线AB和PD所成的角.(11分)

所以异面直线AB和PD所成角的大小arctan3.(14分)
分析:(1)先设底面边长为a,斜高为H,由题意a与H的关系,求得正四棱锥体积V的表达式,最后利用基本不等式求其最大值即可;
(2)先根据异面直线及其所成的角的定义得出∠PDQ即为异面直线AB和PD所成的角再在直角三角形中求出其正切值即得异面直线AB和PD所成角的大小.
点评:本题是中档题,考查直线与平面所成角的求法、棱柱、棱锥、棱台的体积,考查空间想象能力,计算能力,熟练掌握基本定理、基本方法是解决本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
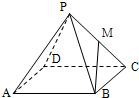
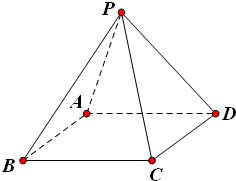 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
 ,M是侧棱PC的中点,则异面直线PA与BM所成角为 .
,M是侧棱PC的中点,则异面直线PA与BM所成角为 .