题目内容
对于任意实数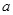 (
(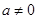 )和
)和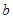 ,不等式
,不等式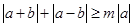 恒成立,记实数
恒成立,记实数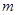 的最大值为
的最大值为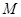 。
。
(1)求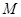 的值;
的值;
(2)解不等式: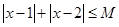 。
。
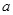 (
(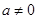 )和
)和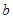 ,不等式
,不等式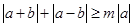 恒成立,记实数
恒成立,记实数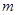 的最大值为
的最大值为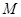 。
。(1)求
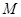 的值;
的值;(2)解不等式:
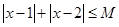 。
。(1) 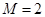
(2)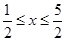
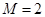
(2)
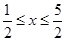
试题分析:解:(I)不等式
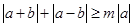 恒成立,即不等式
恒成立,即不等式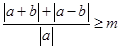 对任意实数
对任意实数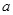 (
(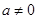 )和
)和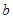 恒成立。 …………2分
恒成立。 …………2分由于
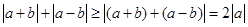
当且仅当
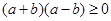 时取等号,即
时取等号,即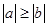 时。
时。所以有:
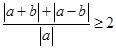
即:
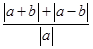 的最小值为2。于是
的最小值为2。于是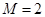 。 …………5分
。 …………5分(II)不等式即
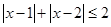
由于
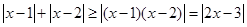
原不等式等价于:
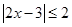
解得:
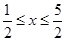 。 …………10分
。 …………10分点评:主要是利用绝对值不等式的性质来放缩短到最值的求解以及结合几何意义来得到不等式恒成立问题的运用,属于基础题。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
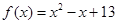 ,实数
,实数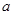 满足
满足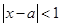 ,求证:
,求证: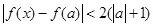 .
.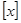 表示不超过
表示不超过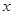 的最大整数。例如
的最大整数。例如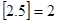 、
、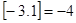 ,当
,当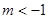 时,有
时,有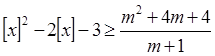 恒成立,则
恒成立,则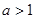 ,则
,则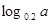 、
、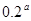 、
、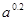 的大小关系是( )
的大小关系是( ) 



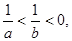 则下列不等式:①
则下列不等式:①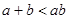 ②
②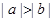 ③
③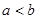 ④
④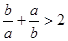 中,正确的不等式有( )
中,正确的不等式有( ) ,
, ,
, ,则
,则 



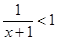 (2)
(2)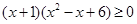
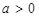 且满足不等式
且满足不等式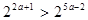 。
。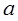 的取值范围。
的取值范围。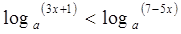 。
。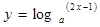 在区间
在区间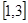 有最小值为
有最小值为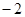 ,求实数
,求实数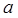 值。
值。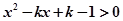 对
对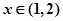 恒成立,则实数
恒成立,则实数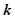 的取值范围是______.
的取值范围是______.