题目内容
7. 已知函数f(x)=Acos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中M,P分别是函数f(x)的图象与坐标轴的交点,N是函数f(x)的图象的一个最低点,若点N,P的横坐标分别为$\frac{5π}{8}$,$\frac{11π}{8}$,且$\overrightarrow{OM}$•$\overrightarrow{ON}$=-2$\sqrt{2}$,则下列说法正确的个数为( )
已知函数f(x)=Acos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中M,P分别是函数f(x)的图象与坐标轴的交点,N是函数f(x)的图象的一个最低点,若点N,P的横坐标分别为$\frac{5π}{8}$,$\frac{11π}{8}$,且$\overrightarrow{OM}$•$\overrightarrow{ON}$=-2$\sqrt{2}$,则下列说法正确的个数为( )①A=±2;
②函数f(x)在[$\frac{9π}{4}$,$\frac{21π}{8}$]上单调递减;
③要得到函数f(x)的图象,只需将函数y=4sinxcosx的图象向左平移$\frac{π}{8}$个单位.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由周期求得ω,由五点法作图求出φ的值,再利用$\overrightarrow{OM}$•$\overrightarrow{ON}$=-2$\sqrt{2}$以及两个向量的数量积的定义,求得A,可得函数f(x)的解析式,从而得出结论.
解答 解:结合函数f(x)=Acos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象,
根据点N,P的横坐标分别为$\frac{5π}{8}$,$\frac{11π}{8}$,可得$\frac{3T}{4}$=$\frac{3}{4}$•$\frac{2π}{ω}$=$\frac{11π}{8}$-$\frac{5π}{8}$,求得ω=2,f(x)=Acos(2x+φ).
①假设A>0,再根据五点法作图可得2•$\frac{5π}{8}$+φ=π,求得φ=-$\frac{π}{4}$,∴f(x)=Acos(2x-$\frac{π}{4}$).
故M(0,$\frac{\sqrt{2}}{2}$A),N($\frac{5π}{8}$,-A).
∵$\overrightarrow{OM}$•$\overrightarrow{ON}$=0-$\frac{\sqrt{2}}{2}$•A2=-2$\sqrt{2}$,∴A=2,f(x)=2cos(2x-$\frac{π}{4}$).
当x∈[$\frac{9π}{4}$,$\frac{21π}{8}$]时,2x-$\frac{π}{4}$∈[$\frac{17π}{4}$,5π],满足f(x)单调递减,故②正确.
要得到函数f(x)=2cos(2x-$\frac{π}{4}$)的图象,只需将函数y=4sinxcosx=2sin2x的图象向右平移$\frac{π}{8}$个单位,
故③不正确.
②若a<0,根据函数的可得2•$\frac{5π}{8}$+φ=2π,k∈Z,求得 φ=$\frac{3π}{4}$,不满足|φ|<$\frac{π}{2}$,故①不正确,
综上可得,只有②正确,
故选:B.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,再利用两个向量的数量积的定义,求得A,体现了分类讨论的数学思想,属于中档题.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案| A. | [-1,1] | B. | [0,2] | C. | [-2,0] | D. | [-2,2] |
| A. | (1,+∞) | B. | (-∞,1) | C. | (-1,1) | D. | (1,3) |
| A. | (0,+∞) | B. | (-∞,1) | C. | (1,+∞) | D. | (0,1) |
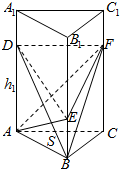 如图,在直三棱柱ABC-A1B1C1中,底面积为S,点D,E,F在侧棱AA1,BB1,CC1上,且AD=h1,BE=h2,CF=h3,求几何体ABC-DEF的体积.
如图,在直三棱柱ABC-A1B1C1中,底面积为S,点D,E,F在侧棱AA1,BB1,CC1上,且AD=h1,BE=h2,CF=h3,求几何体ABC-DEF的体积.