题目内容

2．计算-sin133°cos197°-cos47°cos73°的结果为$\frac{1}{2}$．

分析 由诱导公式把原式等价转化为sin47°cos17°-cos47°sin17°，再由两角和与差的正弦函数能求出结果．

解答 解：-sin133°cos197°-cos47°cos73°
=sin47°cos17°-cos47°sin17°
=sin（47°-17°）
=sin30°
=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．

点评 本题考查三角函数值的求法，是基础题，解题时要认真审题，注意诱导公式和两角和与差的正弦函数公式的合理运用．

练习册系列答案
相关题目
12．己知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，其中左焦点F（-2，0）．
（1）求椭圆C的方程；
（2）若直线y=x+m（m＞0）与椭圆C交于不同的两点A，B，且线段AB的中点M在圆x2+y2=1上，求|AB|．
13．已知实数x、y、z满足x+y+z=0，x2+y2+z2=1，则x的最大值为$\frac{\sqrt{6}}{3}$．
10．已知log${\;}_{\frac{2}{3}}$a＞1，（$\frac{2}{3}$）b＞1，2c=3，则（　　）
A．a＞b＞cB．c＞b＞aC．a＞c＞bD．c＞a＞b
17．设数列{an}的前n项和Sn，a203-a204=a202=1，an+an+1+an+2=4，则S200等于（　　）
A．264B．267C．266D．265
7．已知函数f（x）=Acos（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，其中M，P分别是函数f（x）的图象与坐标轴的交点，N是函数f（x）的图象的一个最低点，若点N，P的横坐标分别为$\frac{5π}{8}$，$\frac{11π}{8}$，且$\overrightarrow{OM}$•$\overrightarrow{ON}$=-2$\sqrt{2}$，则下列说法正确的个数为（　　）
①A=±2；
②函数f（x）在[$\frac{9π}{4}$，$\frac{21π}{8}$]上单调递减；
③要得到函数f（x）的图象，只需将函数y=4sinxcosx的图象向左平移$\frac{π}{8}$个单位．
A．0B．1C．2D．3
14．设连续函数f（x）的定义域为R，已知，若函数f（x）无零点，则f（x）＞0或f（x）＜0恒成立．
（1）用反证法证明：“若存在实数x0，使得f（f（x0））=x0，则至少存在一个实数a，使得f（a）=a”；
（2）若f（x）=ex-$\frac{1}{{e}^{x}}$+x2-2cosx-mx-2，有且仅有一个实数x0，使得f（f（x0））=x0，求实数m的取值范围．
11．已知数列{an}满足a1=$\frac{1}{2}$，$\frac{{a}_{n}+1}{{a}_{n+1}-1}$-$\frac{1}{{a}_{n}-1}$=0，n∈N*．求数列{an}的通项公式．
12．如图，终边落在直线y=±x上的角α的集合是（　　）
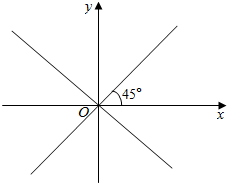
A．{α|α=k•360°+45°，k∈Z}B．{α|α=k•180°+45°，k∈Z}
C．{α|α=k•180°-45°，k∈Z}D．{α|α=k•90°+45°，k∈Z}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网