题目内容
6.在棱锥P-ABC中,侧棱PA,PB,PC两两垂直,若已知PA=3,PB=4,PC=5则三棱锥P-ABC的外接球的表面积为50π.分析 以PA、PB、PC为过同一顶点的三条棱,作长方体如图,则长方体的外接球同时也是三棱锥P-ABC外接球.算出长方体的对角线即为球直径,结合球的表面积公式,可算出三棱锥P-ABC外接球的表面积.
解答  解:以PA、PB、PC为过同一顶点的三条棱,作长方体如图
解:以PA、PB、PC为过同一顶点的三条棱,作长方体如图
则长方体的外接球同时也是三棱锥P-ABC外接球.
∵长方体的对角线长为$\sqrt{{3}^{2}+{4}^{2}+{5}^{2}}$=5$\sqrt{2}$,
∴球直径为5$\sqrt{2}$,半径R=$\frac{5\sqrt{2}}{2}$,
因此,三棱锥P-ABC外接球的表面积是4πR2=4π×($\frac{5\sqrt{2}}{2}$)2=50π
故答案为:50π
点评 本题给出三棱锥的三条侧棱两两垂直,求它的外接球的表面积,着重考查了长方体对角线公式和球的表面积计算等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列说法中,正确的是( )
| A. | 线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$所表示的直线必经过点 ($\overline{x}$,$\overline{y}$) | |
| B. | 一组数据的标准差是这组数据的方差的平方 | |
| C. | 数据4、6、6、7、9、4的众数是4 | |
| D. | 频率分布直方图中各小长方形的面积等于相应各组的频数 |
18.如果袋中有六个红球,四个白球,从中任取一球,确认颜色后放回,重复摸取四次,设X为取得红球的次数,那么X的均值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{12}{5}$ | C. | $\frac{19}{7}$ | D. | $\frac{1}{3}$ |
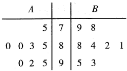 有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.
有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示. 如图,在四棱锥P-ABCD中,底面ABCD是梯形,DC∥AB,DC=2AB,O为AC与BD的交点,E是棱PA上一点,且OE∥平面PBC,求$\frac{AE}{PE}$的值.
如图,在四棱锥P-ABCD中,底面ABCD是梯形,DC∥AB,DC=2AB,O为AC与BD的交点,E是棱PA上一点,且OE∥平面PBC,求$\frac{AE}{PE}$的值.