题目内容
【题目】2012年12月18日,作为全国首批开展空气质量新标准监测的74个城市之一,郑州市正式发布![]() 数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(
数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(![]() ),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的
),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的![]() 的平均值为依据,播报我市的空气质量.
的平均值为依据,播报我市的空气质量.
(Ⅰ)若某日播报的![]() 为118,已知轻度污染区
为118,已知轻度污染区![]() 的平均值为74,中度污染区
的平均值为74,中度污染区![]() 的平均值为114,求重度污染区
的平均值为114,求重度污染区![]() 的平均值;
的平均值;
(Ⅱ)如图是2018年11月的30天中![]() 的分布,11月份仅有一天
的分布,11月份仅有一天![]() 在
在![]() 内.
内.
组数 | 分组 | 天数 |
第一组 |
| 3 |
第二组 |
| 4 |
第三组 |
| 4 |
第四组 |
| 6 |
第五组 |
| 5 |
第六组 |
| 4 |
第七组 |
| 3 |
第八组 |
| 1 |
①郑州市某中学利用每周日的时间进行社会实践活动,以公布的![]() 为标准,如果
为标准,如果![]() 小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
②在“创建文明城市”活动中,验收小组把郑州市的空气质量作为一个评价指标,从当月的空气质量监测数据中抽取3天的数据进行评价,设抽取到![]() 不小于180的天数为
不小于180的天数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(Ⅰ)172(Ⅱ)①![]() ②见解析
②见解析
【解析】
(Ⅰ)设重度污染区AQI的平均值为x,利用加权平均数求出x的值;
(Ⅱ)①由题意知11月份AQI小于180的天数,计算所求的概率即可;
②由题意知随机变量X的可能取值,计算对应的概率值,写出分布列,求出数学期望值.
(Ⅰ)设重度污染区![]() 的平均值为
的平均值为![]() ,则
,则![]() ,解得
,解得![]() .
.
即重度污染区![]() 平均值为172.
平均值为172.
(Ⅱ)①由题意知,![]() 在
在![]() 内的天数为1,
内的天数为1,
由图可知,![]() 在
在![]() 内的天数为17天,故11月份
内的天数为17天,故11月份![]() 小于180的天数为
小于180的天数为![]() ,
,
又![]() ,则该学校去进行社会实践活动的概率为
,则该学校去进行社会实践活动的概率为![]() .
.
②由题意知,![]() 的所有可能取值为0,1,2,3,且
的所有可能取值为0,1,2,3,且
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
数学期望![]()
![]()
![]() .
.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】某调查机构对某校学生做了一个是否同意生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”,现已得知100人中同意父母生“二孩”占60%,统计情况如下表:
同意 | 不同意 | 合计 | |
男生 | a | 5 | |
女生 | 40 | d | |
合计 | 100 |
(1)求 a,d 的值,根据以上数据,能否有97.5%的把握认为是否同意父母生“二孩”与性别有关?请说明理由;
(2)将上述调查所得的频率视为概率,现在从所有学生中,采用随机抽样的方法抽取4 位学生进行长期跟踪调查,记被抽取的4位学生中持“同意”态度的人数为 X,求 X 的分布列及数学期望.
附: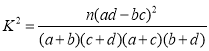
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】新高考,取消文理科,实行“![]() ”,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人(把年龄在
”,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人(把年龄在![]() 称为中青年,年龄在
称为中青年,年龄在![]() 称为中老年),并把调查结果制成下表:
称为中老年),并把调查结果制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 15 | 10 | 10 | 5 | 5 |
了解 | 4 | 12 | 6 | 5 | 2 | 1 |
(1)分别估计中青年和中老年对新高考了解的概率;
(2)请根据上表完成下面![]() 列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
了解新高考 | 不了解新高考 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
附: .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(3)若从年龄在![]() 的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为
的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为![]() ,求
,求![]() 的分布列以及
的分布列以及![]() .
.
【题目】在2016年8月巴西里约热内卢举办的第31届奥运会上,乒乓球比赛团体决赛实行五场三胜制,且任何一方获胜三场比赛即结束.甲、乙两个代表队最终进入决赛,根据双方排定的出场顺序及以往战绩统计分析,甲队依次派出的五位选手分别战胜对手的概率如下表:
出场顺序 | 1号 | 2号 | 3号 | 4号 | 5号 |
获胜概率 |
|
|
|
|
|
若甲队横扫对手获胜(即3∶0获胜)的概率是![]() ,比赛至少打满4场的概率为
,比赛至少打满4场的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求甲队获胜场数的分布列和数学期望.

