题目内容
18.已知正实数x,y满足$\frac{1}{1+2x}$+$\frac{1}{1+3y}$=$\frac{1}{2}$,则xy的最小值等于$\frac{9}{4}$.分析 由于正实数x,y满足条$\frac{1}{1+2x}$+$\frac{1}{1+3y}$=$\frac{1}{2}$,用x表示y,构造函数f(x)=xy,再利用导数研究函数的单调性极值与最值即可得出.
解答 解:由$\frac{1}{1+2x}$+$\frac{1}{1+3y}$=$\frac{1}{2}$,解得:y=$\frac{2x+3}{3(2x-1)}$>0,x>$\frac{1}{2}$,
∴xy=$\frac{x(2x+3)}{3(2x-1)}$=f(x),
∴f′(x)=$\frac{3(2x+1)(2x-3)}{{(6x-3)}^{2}}$,(x>$\frac{1}{2}$),
令f′(x)>0,解得:x>$\frac{3}{2}$,令f′(x)<0,解得:$\frac{1}{2}$<x$\frac{3}{2}$,
∴函数f(x)在($\frac{1}{2}$,$\frac{3}{2}$)递减,在($\frac{3}{2}$,+∞)递增,
∴f(x)最小值=f($\frac{3}{2}$)=$\frac{9}{4}$,
故答案为:$\frac{9}{4}$.
点评 本题考查了利用导数研究函数的单调性极值与最值,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
13.已知a为如图所示的算法框图中输出的结果,则二项式${(x+\frac{a}{x^2})^9}$的展开式中的常数项为( )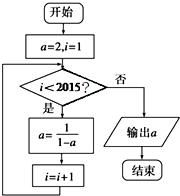

| A. | 84 | B. | -84 | C. | 672 | D. | -672 |
8.已知抛物线C:y2=2px(p>0)的焦点F(1,0),若点P在抛物线C上运动,点Q在直线x+y+5=0上运动,则|PQ|的最小值为( )
| A. | $\frac{9\sqrt{2}}{4}$ | B. | $\frac{19\sqrt{2}}{8}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
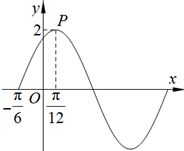 f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(0)=$\sqrt{3}$.
f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(0)=$\sqrt{3}$.