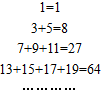题目内容
7.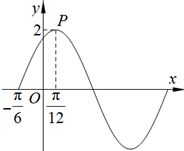 f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(0)=$\sqrt{3}$.
f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(0)=$\sqrt{3}$.
分析 根据图象知A,以及周期,求出ω和φ即可得到结论.
解答 解:由图象知A=2,函数的周期T=4×[$\frac{π}{12}$-($-\frac{π}{6}$)]=4×$\frac{3π}{12}$=π,
∵T=$\frac{2π}{ω}=π$,
∴ω=2,
则f(x)=2sin(2x+φ),
由五点对应法知2×$\frac{π}{12}$+φ=$\frac{π}{2}$,
解得φ=$\frac{π}{2}$-$\frac{π}{6}$=$\frac{π}{3}$,
则f(x)=2sin(2x+$\frac{π}{3}$),
则f(0)=2sin$\frac{π}{3}$=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$
点评 本题主要考查三角函数解析式的求解,利用函数图象求出A,ω和φ的值是解决本题的关键.

练习册系列答案
相关题目
12.如图的程序框图表示求式子1×3×7×15×31×63的值,则判断框内可以填的条件为( )
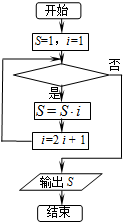

| A. | i≤31? | B. | i≤63? | C. | i≥63? | D. | i≤127? |
17.由于工业化城镇化的推进,大气污染日益加重,空气质量逐步恶化,雾霾天气频率增大,大气污染可引起心悸、胸闷等心脏病症状.为了解某市患心脏病是否与性别有关,在某医院心血管科随机的对入院50位进行调查得到了如下列联表:问有多大的把握认为是否患心脏病与性别有关.答( )
(参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 患心脏病 | 不患心脏病 | 合计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 95% | B. | 99% | C. | 99.5% | D. | 99.9% |