题目内容
已知定义域为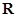 的函数
的函数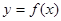 满足
满足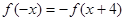 , 当
, 当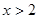 时,
时,
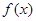 单调递增,若
单调递增,若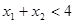 且
且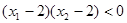 ,则
,则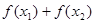 的值 ( )
的值 ( )
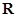 的函数
的函数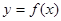 满足
满足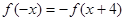 , 当
, 当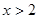 时,
时,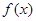 单调递增,若
单调递增,若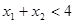 且
且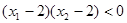 ,则
,则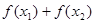 的值 ( )
的值 ( )| A.恒大于0 | B.恒小于0 | C.可能等于0 | D.可正可负 |
B
分析:先通过给定条件确定函数为关于点(2,0)成中心对称,再由图象可得答案.
解答:解:由函数y=f(x)满足f(-x)=-f(x+4)得函数的图象关于点(2,0)对称,

由x1+x2<4且(x1-2)(x2-2)<0不妨设x1>2,x2<2,
借助图象可得f(x1)+f(x2)的值恒小于0,
故选B.
解答:解:由函数y=f(x)满足f(-x)=-f(x+4)得函数的图象关于点(2,0)对称,

由x1+x2<4且(x1-2)(x2-2)<0不妨设x1>2,x2<2,
借助图象可得f(x1)+f(x2)的值恒小于0,
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
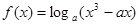
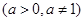 在区间
在区间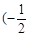 ,0)内单调递增,则
,0)内单调递增,则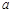 的
的 ,1)
,1) ,1)
,1) ,
,
 )
)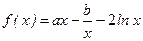 ,且
,且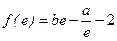 (
(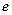 为自然对数的底数)。
为自然对数的底数)。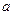 与
与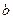 的关系;
的关系;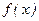 在其定义域内为增函数,求
在其定义域内为增函数,求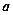 的取值范围;
的取值范围;
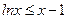 )
)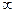 )上单调递增,并且f (x)<0对
)上单调递增,并且f (x)<0对 一切
一切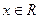 成立,试判断
成立,试判断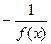 在(-
在(-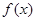 满足:①定义域为
满足:①定义域为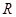 ;②对任意
;②对任意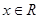 ,有
,有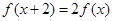 ;③当
;③当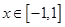 时,
时,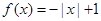 .则方程
.则方程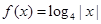 在区间
在区间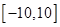 内的解的个数
内的解的个数 满足:对一切
满足:对一切 当
当 时,
时, ,则
,则 ( )
( )



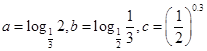 ,则
,则



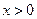 时,函数
时,函数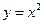 与函数
与函数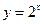 的图像所围成的封闭区域的面积是
的图像所围成的封闭区域的面积是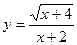 的定义域为
的定义域为 