题目内容
(本题满分15分)
已知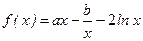 ,且
,且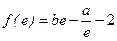 (
(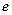 为自然对数的底数)。
为自然对数的底数)。
(1)求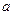 与
与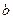 的关系;
的关系;
(2)若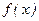 在其定义域内为增函数,求
在其定义域内为增函数,求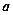 的取值范围;
的取值范围;
(3)证明:
(提示:需要时可利用恒等式: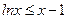 )
)
已知
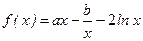 ,且
,且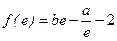 (
(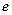 为自然对数的底数)。
为自然对数的底数)。(1)求
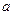 与
与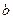 的关系;
的关系;(2)若
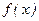 在其定义域内为增函数,求
在其定义域内为增函数,求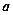 的取值范围;
的取值范围;(3)证明:

(提示:需要时可利用恒等式:
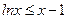 )
)解:(1)由题意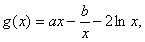
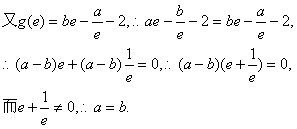
(2)由(1)知: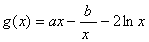 (x>0)
(x>0)
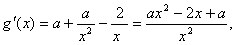
令h(x)=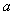 x2-2x+
x2-2x+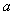 .要使g(x)在(0,+∞)为增函数,只需h(x)在(0,+∞)满足:
.要使g(x)在(0,+∞)为增函数,只需h(x)在(0,+∞)满足:
h(x)≥0恒成立.
 即
即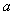 x2-2x+
x2-2x+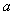 ≥0
≥0
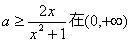 上恒成立
上恒成立
又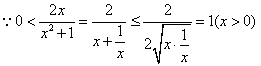
所 以
以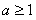
(3)证明:证:lnx-x+1≤0 (x>0),
设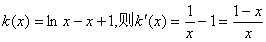 .
.
当x∈(0,1)时,k′(x)>0,∴k(x)为单调递增函数;
当x∈(1,∞)时,k′(x)<0,∴k(x)为单调递减函 数;
数;
∴x=1为k(x)的极大值点,
∴k(x)≤k(1)=0.
即lnx-x+1≤0,∴lnx≤x-1.
②由①知lnx≤x-1,又x>0,
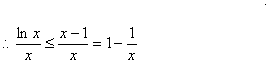

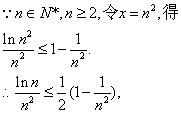
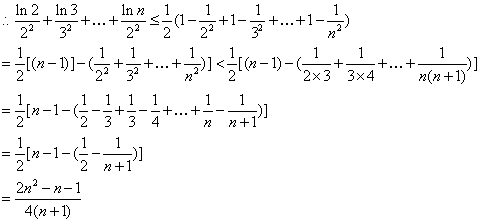
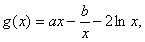
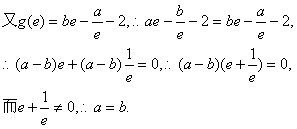
(2)由(1)知:
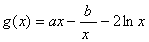 (x>0)
(x>0)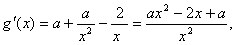
令h(x)=
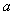 x2-2x+
x2-2x+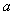 .要使g(x)在(0,+∞)为增函数,只需h(x)在(0,+∞)满足:
.要使g(x)在(0,+∞)为增函数,只需h(x)在(0,+∞)满足:h(x)≥0恒成立.
 即
即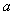 x2-2x+
x2-2x+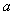 ≥0
≥0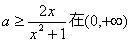 上恒成立
上恒成立又
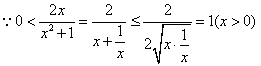
所
 以
以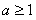
(3)证明:证:lnx-x+1≤0 (x>0),
设
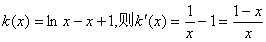 .
.当x∈(0,1)时,k′(x)>0,∴k(x)为单调递增函数;
当x∈(1,∞)时,k′(x)<0,∴k(x)为单调递减函
 数;
数;∴x=1为k(x)的极大值点,
∴k(x)≤k(1)=0.
即lnx-x+1≤0,∴lnx≤x-1.
②由①知lnx≤x-1,又x>0,
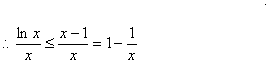

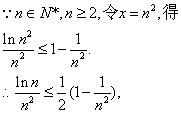
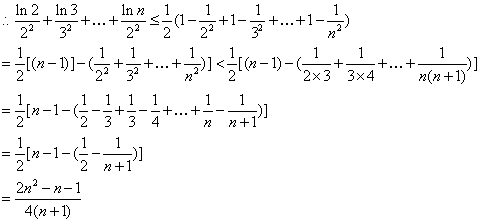
略

练习册系列答案
相关题目
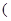
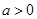 且
且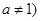 在
在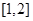 上的最大值与最小值之和为
上的最大值与最小值之和为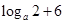 ,则
,则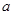 的值为 ( )
的值为 ( )



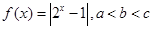 ,且
,且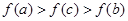 ,则下列结论中,必成立的是( )
,则下列结论中,必成立的是( )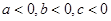

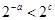
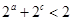
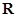 的函数
的函数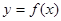 满足
满足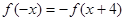 , 当
, 当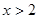 时,
时,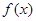 单调递增,若
单调递增,若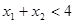 且
且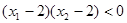 ,则
,则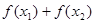 的值 ( )
的值 ( ) ,则f(
,则f( )等于( )
)等于( )
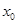 是方程式
是方程式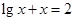 的解,则
的解,则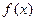 是定义在R上的奇函数,当x≤0时,
是定义在R上的奇函数,当x≤0时,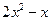 ,则
,则
 上的函数
上的函数 是偶函数,且
是偶函数,且 时,
时, ,(1)当
,(1)当 时,求
时,求 解析式;(2)写出
解析式;(2)写出
 和
和