题目内容

7．已知命题p：?α∈R，cos（π-α）=cosα；命题q：?x∈R，x2+1＞0．则下面结论正确的是（　　）
A．￢q是真命题B．p 是假命题C．p∧q是假命题D．p∨q是真命题

分析 分别判断命题p，q的真假即可．

解答 解：∵cos（π-α）=-cosα，
∴若cos（π-α）=cosα，
则-cosα=cosα，
即cosα=0，即可，故命题p为真命题．，
题q：?x∈R，x2+1＞0为真命题．
则p∨q是真命题，其余为假命题．
故选：D．

点评 本题主要考查复合命题的真假判断，根据条件判断题p，q的真假是解决本题的关键．

练习册系列答案
相关题目
17．某企业有两个分厂生产某种零件，按规定内径尺寸（单位：mm）的值落在（29.94，30.06）的零件为优质品．从两个分厂生产的零件中抽出500件，量其内径尺寸的结果如表：
甲厂
分组[29.86，
29.90）		[29.90，
29.94）		[29.94，
29.98）		[29.98，
30.02）		[30.02，
30.06）		[30.06，
30.10）		[30.10，
30.14）
频数12638618292614
乙厂
分组[29.86，
29.90）		[29.90，
29.94）		[29.94，
29.98）		[29.98，
30.02）		[30.02，
30.06）		[30.06，
30.10）		[3 0.10，
30.14）
频数297185159766218
（1）试分别估计两个分厂生产的零件的优质品率；
（2）由于以上统计数据填下面2×2列联表，并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”．
甲厂乙厂合计
优质品   
非优质品   
合计   
下面的临界值表供参考：（参考公式：K2=$\frac{{n（ad-bc）}^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
P=（K2≥k0）0.150.100.05[0.0250.0100.0050.001
k02.0722.7063.8415.0246.6357.87910.828
18．已知6件产品中有2件次品，今从中任取2件，在已知其中一件是次品的前提下，另一件也是次品的概率为（　　）
A．$\frac{1}{15}$B．$\frac{1}{9}$C．$\frac{3}{5}$D．$\frac{3}{10}$
15．已知直线x+y-k=0（k＞0）与圆x2+y2=4交于不同的两点A、B，O是坐标原点，若$|{\overrightarrow{OA}+\overrightarrow{OB}}|=\frac{{\sqrt{3}}}{3}|{\overrightarrow{AB}}|$，则实数k=（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2
2．在锐角△ABC中，角A，B，C的对边分别是a，b，c，若A=2B，则$\frac{c}{b}$的取值范围是（　　）
A．（1，3）B．（2，3）C．（0，3）D．（1，2）
12．化简：$\frac{sin（θ-π）si{n}^{2}（θ+\frac{π}{2}）tan（θ+3π）}{cos（2π-θ）cos（-\frac{3π}{2}+θ）sin（π+θ）}$．
19．已知结合集合A={x|1≤3x＜9}，B={y|y=sinx，x∈R}，则A∩B=（　　）
A．[0，1）B．[0，1]C．（0，1）D．[-1，2）
16．如图1所示的茎叶图是青年歌手电视大奖赛中7位评委给参加最后决赛的两位选手甲、乙评定的成绩，程序框图（图2）用来编写程序统计每位选手的成绩（各评委所给有效分数的平均值），试根据下面条件回答下列问题：

（1）根据茎叶图，乙选手的成绩中，中位数和众数分别是多少？
（2）在程序框图中，用k表示评委人数，用a表示选手的最后成绩（各评委所给有效分数的平均值）．那么图中①②处应填什么？“S1=S-max-min”的含义是什么？
（3）根据程序框图，甲、乙的最后成绩分别是多少？
（4）从甲、乙的有效分数中各取一个分数分别记作为x，y，若甲、乙的最后成绩分别是a，b，求“|x-a|≤1且|y-b|≤1”的概率．
17．执行如图所示的程序框图，则输出的T值为（　　）
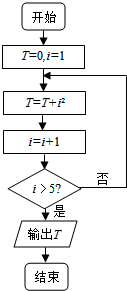
A．30B．54C．55D．91

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网