题目内容
某企业为更好地了解设备改造前后与生产合格品的关系,随机抽取了100件产品进行分析,但由于工作人员不小心,丢失了部分数据:
设备改造效果分析列联表

工作人员从设备改造前生产的产品中抽取两件,合格品数为ξ,从设备改造后生产的产品中抽取两件,合格品数为η,经计算得: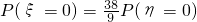 .
.
(1)填写列联表中缺少的数据;
(2)求出ξ与η的数学期望,并比较大小,请解释你所得出结论的实际意义;
(3)能够以97.5%的把握认为设备改造有效吗?
参考数据:
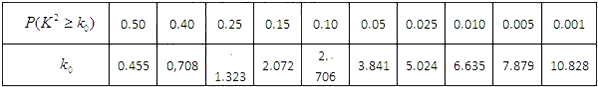
解:(1)工作人员从设备改造前生产的产品中抽取两件,合格品数为ξ,
从设备改造后生产的产品中抽取两件,合格品数为η
∵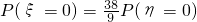 .
.
∴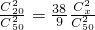 ,
,
∴x=10,y=50-10=40,M=20+10=30,N=30+40=70.
(2)由题意知ξ可能取值是0,1,2
P(ξ=0)=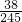 ,
,
P(ξ=1)= ,
,
P(ξ=2)=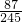
∴ξD的分布列是
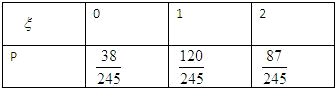
∴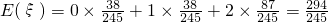
由题意知η的可能取值是0,1,2
P(η=0)=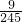 ,
,
P(η=1)= ,
,
P(η=2)=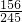
∴η的分布列是
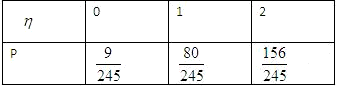
∴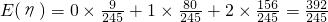
∵E(ξ)<E(η),
∴设备改造是有效的.
(3)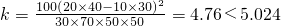 ,
,
∴不能以97.5%的把握认为设备改造有效.
分析:(1)工作人员从设备改造前生产的产品中抽取两件,合格品数为ξ,从设备改造后生产的产品中抽取两件,合格品数为η,根据所给的两个变量取0时概率之间的关系,写出关于x的方程,解方程即可,在再根据列联表中数据的关系,得到结果.
(2)根据题意看出两个变量可能取值,ξ可能取值是0,1,2,η的可能取值是0,1,2,结合变量对应的事件写出两组变量的分布列,算出期望,比较两个期望值的大小,得到结论.
(3)根据列联表所给的数据,代入求观测值的公式,做出观测值是4.76,同临界值进行比较,4.76<5.024,得到不能以97.5%的把握认为设备改造有效.
点评:本题考查离散型随机变量的分布列和期望,考查独立性检验,是一个统计和概率的综合题,本题难易可以作为一个高考题目.
从设备改造后生产的产品中抽取两件,合格品数为η
∵
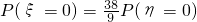 .
.∴
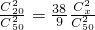 ,
,∴x=10,y=50-10=40,M=20+10=30,N=30+40=70.
(2)由题意知ξ可能取值是0,1,2
P(ξ=0)=
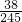 ,
,P(ξ=1)=
 ,
,P(ξ=2)=
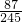
∴ξD的分布列是
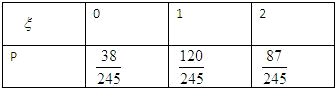
∴
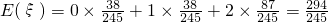
由题意知η的可能取值是0,1,2
P(η=0)=
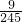 ,
,P(η=1)=
 ,
,P(η=2)=
∴η的分布列是
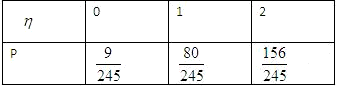
∴
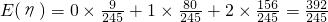
∵E(ξ)<E(η),
∴设备改造是有效的.
(3)
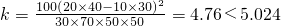 ,
,∴不能以97.5%的把握认为设备改造有效.
分析:(1)工作人员从设备改造前生产的产品中抽取两件,合格品数为ξ,从设备改造后生产的产品中抽取两件,合格品数为η,根据所给的两个变量取0时概率之间的关系,写出关于x的方程,解方程即可,在再根据列联表中数据的关系,得到结果.
(2)根据题意看出两个变量可能取值,ξ可能取值是0,1,2,η的可能取值是0,1,2,结合变量对应的事件写出两组变量的分布列,算出期望,比较两个期望值的大小,得到结论.
(3)根据列联表所给的数据,代入求观测值的公式,做出观测值是4.76,同临界值进行比较,4.76<5.024,得到不能以97.5%的把握认为设备改造有效.
点评:本题考查离散型随机变量的分布列和期望,考查独立性检验,是一个统计和概率的综合题,本题难易可以作为一个高考题目.

练习册系列答案
相关题目
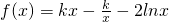 .
.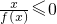 的解集.
的解集.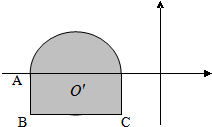 已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).
已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).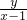 的取值范围;
的取值范围; +
+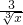 )n的展开式中,各项系数的和与其各项二项式系数的和之比为64,则(1-x)n的展开式中系数最小的项的系数等于 ________.
)n的展开式中,各项系数的和与其各项二项式系数的和之比为64,则(1-x)n的展开式中系数最小的项的系数等于 ________. ,则φ=________;此时函数的图象的对称点为 ________.
,则φ=________;此时函数的图象的对称点为 ________. >
>
 )a>(
)a>(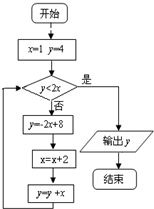 执行如图的程序框图,输出的y=________.
执行如图的程序框图,输出的y=________.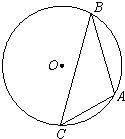 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.) ,
,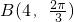 间的距离是________.
间的距离是________.