Question

函数f（x）=sin（2x+φ）（-π＜φ＜0）的图象的一条对成轴是，则φ=________；此时函数的图象的对称点为 ________．

Answer 1

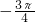
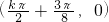    k∈Z
分析：函数的对称轴，就是函数取得最值点的x值，结合题意求解即可；对称点就是函数与x轴的交点坐标，就是y=0时，的x值．
解答：函数f（x）=sin（2x+φ）（-π＜φ＜0）的图象的一条对成轴是，
所以sin（+φ）=-1，φ=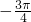
函数为：f（x）=sin（2x+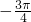），令sin（2x+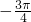）=0
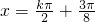所以，k∈Z
故答案为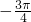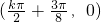：；k∈Z
点评：本题考查正弦函数的对称性，考查计算能力，是基础题．