题目内容
【题目】已知动圆![]() 和定圆
和定圆![]() 外切,和定直线
外切,和定直线![]() 相切.
相切.
(1)求该动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,在曲线
两点,在曲线![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为定值,求出点
为定值,求出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,(2)存在,点
,(2)存在,点![]() .
.
【解析】
(1)由已知可得:点G的轨迹是到定点C(2,0)的距离和到直线L:x=-2的距离相等的点的集合.由抛物线的定义可知:点P的轨迹是抛物线.求出即可.
(2)设出直线![]() 的方程为:
的方程为: ![]() ,联立两方程得
,联立两方程得![]() ,设设
,设设![]() ,得出韦达定理
,得出韦达定理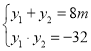 ,设
,设![]() ,表示出
,表示出![]() ,由恒成立的思想可得出定点坐标.
,由恒成立的思想可得出定点坐标.
(1)由圆![]() 可得:圆心
可得:圆心![]() ,半径
,半径![]() .
.
设所求动圆圆心为![]() ,过点
,过点![]() 作
作![]() 垂直于直线:
垂直于直线:![]() ,
,![]() 为垂足.
为垂足.
则![]() ,可得
,可得![]() .
.
因此可得:点![]() 的轨迹是到定点
的轨迹是到定点![]() 的距离和到直线
的距离和到直线![]() 的距离相等的点的集合,
的距离相等的点的集合,
由抛物线的定义可知:点![]() 的轨迹是抛物线,定点
的轨迹是抛物线,定点![]() 为焦点,定直线
为焦点,定直线![]() 是准线.∴抛物线的方程为:
是准线.∴抛物线的方程为:![]() .
.
∴该动圆圆心![]() 的轨迹
的轨迹![]() 的方程是
的方程是![]() .
.
(2) 存在定点![]() 的坐标为
的坐标为![]() ,理由如下,
,理由如下,
设直线![]() 的方程为:
的方程为: ![]() ,由
,由 得,
得,![]() ,整理得
,整理得![]() ,
,
设![]() ,则
,则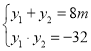 ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴当![]() 时,
时,![]() 为定值
为定值![]() ,此时点
,此时点![]() ,
,
所以在曲线![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为定值,此时点
为定值,此时点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目
【题目】一研学实践活动小组利用课余时间,对某公司1月份至5月份销售某种产品的销售量及销售单价进行了调查,月销售单价![]() (单位:元)和月销售量
(单位:元)和月销售量![]() (单位:百件)之间的一组数据如下表所示:
(单位:百件)之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 |
月销售单价 | 1.6 | 1.8 | 2 | 2.2 | 2.4 |
月销售量 | 10 | 8 | 7 | 6 | 4 |
(1)根据1至5月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)预计在今后的销售中,月销售量与月销售单价仍然服从(1)中的关系,若该种产品的成本是1元/件,那么该产品的月销售单价应定为多少元才能获得最大月利润?(注:利润=销售收入-成本)
(回归直线方程![]() ,其中
,其中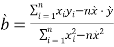 .参考数据:
.参考数据:![]() ,
,![]() )
)