题目内容
【题目】已知几何体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 面
面![]() ,
,![]() ,
,![]() .
.
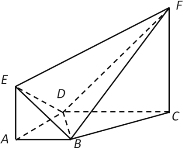
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角E-BD-F的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由勾股定理逆定理证得![]() ,再由已知得
,再由已知得![]() 平面
平面![]() ,
,![]() ,从而有线面垂直,得面面垂直;
,从而有线面垂直,得面面垂直;
(2)分别以DA、DC所在直线为![]() 轴、
轴、![]() 轴,以D为垂足作面DAC的垂线DZ为
轴,以D为垂足作面DAC的垂线DZ为![]() 轴,建系,写出各点坐标,求出二面角两个面的法向量,由法向量夹角的余弦值得二面角的余弦值(注意判断二面角是锐角还是钝角).
轴,建系,写出各点坐标,求出二面角两个面的法向量,由法向量夹角的余弦值得二面角的余弦值(注意判断二面角是锐角还是钝角).
(1)证明:在直角梯形![]() 中由已知可得
中由已知可得![]()
![]()
![]() ,且
,且![]() 面
面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 面
面![]() ,
,![]() ,
,
![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]()
∴![]() 面
面![]()
且![]() 面
面![]() ,故面
,故面![]() 面
面![]() ;
;
(2)分别以DA、DC所在直线为![]() 轴、
轴、![]() 轴,以D为垂足作面DAC的垂线DZ为
轴,以D为垂足作面DAC的垂线DZ为![]() 轴,建系如图
轴,建系如图
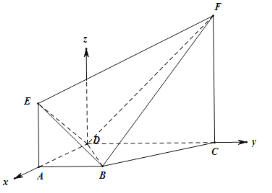
![]() ,
,
则![]() ,
,
设面DEB的法向量为![]() ,
,
则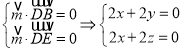 ,
,
取![]() ,则
,则![]() ,故
,故![]()
设面DBF的法向量为![]() ,则
,则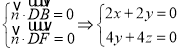 ,
,
取![]() ,则
,则![]() ,故
,故![]()
则![]() ,
,
由图可得二面角E-BD-F的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某汽车制造厂制造了某款汽车.为了了解汽车的使用情况,通过问卷的形式,随机对50名客户对该款汽车的喜爱情况进行调查,如图1是汽车使用年限的调查频率分布直方图,如表2是该50名客户对汽车的喜爱情况.
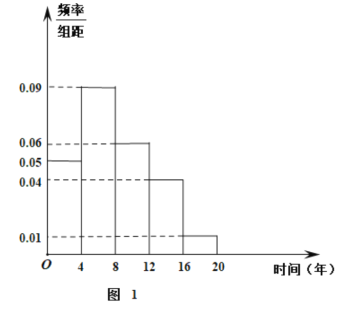
表2
不喜欢该款汽车 | 喜欢该款汽车 | 总计 | |
女士 | 11 | ||
男士 | 23 | 30 | |
总计 |
(1)将表2补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢该款汽车与性别有关;
(2)根据图中的数据,甲说:“中位数在![]() 组内”;乙说:“平均数大于中位数”;丙说:“中位数和平均数一样”,针对三位同学的说法,你认为哪种说法合理,给出说明.
组内”;乙说:“平均数大于中位数”;丙说:“中位数和平均数一样”,针对三位同学的说法,你认为哪种说法合理,给出说明.
附:![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
