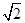题目内容
已知
是直线
被椭圆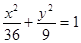
所截得的线段的中点，则直线的方程是( )
A． | B． |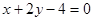
C． | D． |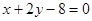
D
解析试题分析：利用“点差法”即可得出直线的斜率，即设直线与椭圆相交于两点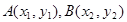
，代入椭圆方程得
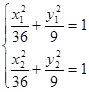，两式相减得
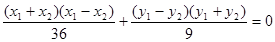，由为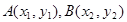两点的中点可知
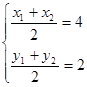代入上式可求直线的斜率，然后利用点斜式即可得出方程．
考点：直线与圆锥曲线的关系．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
已知双曲线
的虚轴长是实轴长的2倍，则实数
的值是( )
A． | B． | C． | D． |
已知抛物线C：
的焦点为
,
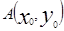是C上一点，
，则
（ ）
| A． 1 | B． 2 | C． 4 | D． 8 |
若实数
满足
，则曲线
与曲线
的（ ）
| A．离心率相等 | B．虚半轴长相等 | C．实半轴长相等 | D．焦距相等 |
双曲线C:
的离心率为2，焦点到渐近线的距离为
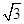，则C的焦距等于( )
| A．2 | B． | C．4 | D． |
(a>0，b>0)的左焦点F(-c，0)作圆x2+y2=a2的切线，切点为E，延长FE交抛物线y2=4cx于点P，O为原点，若|FE|=|EP|，则双曲线离心率为( )
已知点M(－3,0)，N(3,0)，B(1,0)，动圆C与直线MN切于点B，过M、N与圆C相切的两直线相交于点P，则P点的轨迹方程为( )
A．x2－ ＝1(x>1) | B．x2－＝1(x<－1) |
| C．x2＋＝1(x>0) | D．x2－ ＝1(x>1) |
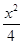＋y2＝1的两个焦点为F1，F2，过F1作垂直于x轴的直线与椭圆相交，一个交点为P，则|PF2|＝( )
＝1的两个焦点，P是双曲线上的一点，且3|PF1|＝4|PF2|，则△PF1F2的面积等于 ( )
