题目内容
已知a∈R,函数f(x)=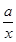 +ln x-1.
+ln x-1.
(1)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)求f(x)在区间(0,e]上的最小值.
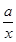 +ln x-1.
+ln x-1.(1)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)求f(x)在区间(0,e]上的最小值.
(1) x-4y+4ln 2-4=0 (2) 当a≤0时,函数f(x)在区间(0,e]上无最小值;
当0<a<e时,函数f(x)在区间(0,e]上的最小值为ln a;
当a≥e时,函数f(x)在区间(0,e]上的最小值为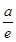 .
.
当0<a<e时,函数f(x)在区间(0,e]上的最小值为ln a;
当a≥e时,函数f(x)在区间(0,e]上的最小值为
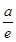 .
.解:(1)当a=1时,f(x)=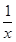 +ln x-1,x∈(0,+∞),
+ln x-1,x∈(0,+∞),
所以f′(x)=-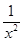 +
+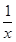 =
=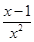 ,x∈(0,+∞).
,x∈(0,+∞).
因此f′(2)=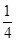 .
.
即曲线y=f(x)在点(2,f(2))处的切线斜率为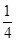 .
.
又f(2)=ln 2-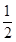 ,
,
所以曲线y=f(x)在点(2,f(2))处的切线方程为y-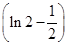 =
=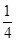 (x-2),
(x-2),
即x-4y+4ln 2-4=0.
(2)因为f(x)=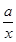 +ln x-1,
+ln x-1,
x∈(0,+∞),
所以f′(x)=- +
+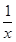 =
=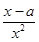 .
.
令f′(x)=0,得x=a.
①若a≤0,则f′(x)>0,函数f(x)在区间(0,e]上单调递增,此时函数f(x)无最小值.
②若0<a<e,则当x∈(0,a)时,f′(x)<0,函数f(x)在区间(0,a)上单调递减;
当x∈(a,e]时,f′(x)>0,函数f(x)在区间(a,e]上单调递增,
所以当x=a时,函数f(x)取得最小值ln a.
③若a≥e,则当x∈(0,e]时,f′(x)≤0,函数f(x)在区间(0,e]上单调递减,
所以当x=e时,函数f(x)取得最小值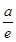 .
.
综上可知,当a≤0时,函数f(x)在区间(0,e]上无最小值;
当0<a<e时,函数f(x)在区间(0,e]上的最小值为ln a;
当a≥e时,函数f(x)在区间(0,e]上的最小值为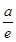 .
.
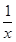 +ln x-1,x∈(0,+∞),
+ln x-1,x∈(0,+∞),所以f′(x)=-
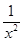 +
+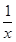 =
=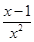 ,x∈(0,+∞).
,x∈(0,+∞).因此f′(2)=
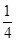 .
.即曲线y=f(x)在点(2,f(2))处的切线斜率为
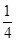 .
.又f(2)=ln 2-
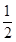 ,
,所以曲线y=f(x)在点(2,f(2))处的切线方程为y-
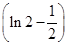 =
=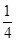 (x-2),
(x-2),即x-4y+4ln 2-4=0.
(2)因为f(x)=
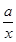 +ln x-1,
+ln x-1,x∈(0,+∞),
所以f′(x)=-
 +
+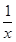 =
=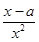 .
.令f′(x)=0,得x=a.
①若a≤0,则f′(x)>0,函数f(x)在区间(0,e]上单调递增,此时函数f(x)无最小值.
②若0<a<e,则当x∈(0,a)时,f′(x)<0,函数f(x)在区间(0,a)上单调递减;
当x∈(a,e]时,f′(x)>0,函数f(x)在区间(a,e]上单调递增,
所以当x=a时,函数f(x)取得最小值ln a.
③若a≥e,则当x∈(0,e]时,f′(x)≤0,函数f(x)在区间(0,e]上单调递减,
所以当x=e时,函数f(x)取得最小值
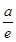 .
.综上可知,当a≤0时,函数f(x)在区间(0,e]上无最小值;
当0<a<e时,函数f(x)在区间(0,e]上的最小值为ln a;
当a≥e时,函数f(x)在区间(0,e]上的最小值为
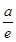 .
.
练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
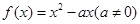 ,
,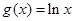 ,
,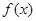 图象与
图象与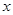 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为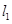 ,
,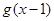 与
与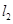 , 并且
, 并且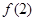 的值;
的值;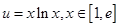 的取值范围及函数
的取值范围及函数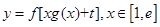 的最小值;
的最小值;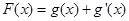 ,给定
,给定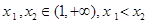 ,对于两个大于1的正数
,对于两个大于1的正数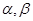 ,存在实数
,存在实数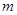 满足:
满足: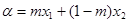 ,
,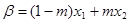 ,并且使得不等式
,并且使得不等式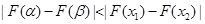 恒成立,求实数
恒成立,求实数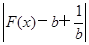 -3有四个零点,求b的取值范围;
-3有四个零点,求b的取值范围;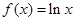 ,
,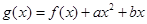 ,其中
,其中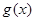 的函数图象在点
的函数图象在点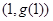 处的切线平行于
处的切线平行于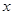 轴.
轴.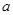 与
与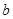 的关系; (2)若
的关系; (2)若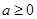 ,试讨论函数
,试讨论函数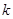 的直线与函数
的直线与函数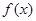 的图象交于两点
的图象交于两点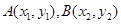 (
(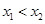 )证明:
)证明: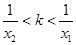 .
.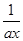 +b(a>0).
+b(a>0).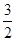 x,求a,b的值.
x,求a,b的值.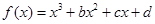 (
(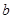 、
、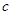 、
、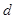 为常数),当
为常数),当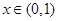 时取极大值,当
时取极大值,当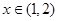 时取极小值,则
时取极小值,则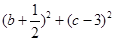 的取值范围是( )
的取值范围是( )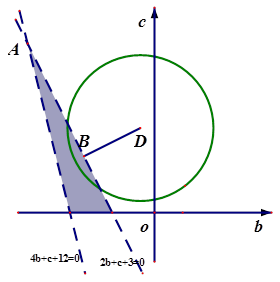
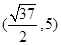
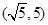
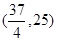
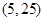
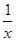 .
.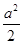 ,当x∈[0,ln 3]时,函数g(x)的最大值M与最小值m的差为
,当x∈[0,ln 3]时,函数g(x)的最大值M与最小值m的差为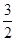 ,则a=________.
,则a=________.