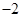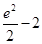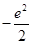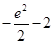题目内容
已知函数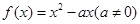 ,
,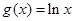 ,
,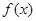 图象与
图象与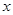 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为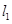 ,
,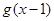 与
与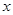 轴的交点N处的切线为
轴的交点N处的切线为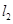 , 并且
, 并且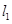 与
与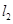 平行.
平行.
(1)求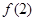 的值;
的值;
(2)已知实数t∈R,求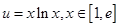 的取值范围及函数
的取值范围及函数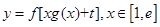 的最小值;
的最小值;
(3)令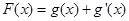 ,给定
,给定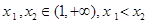 ,对于两个大于1的正数
,对于两个大于1的正数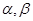 ,存在实数
,存在实数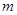 满足:
满足: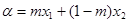 ,
,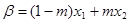 ,并且使得不等式
,并且使得不等式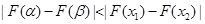 恒成立,求实数
恒成立,求实数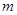 的取值范围.
的取值范围.
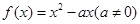 ,
,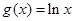 ,
,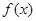 图象与
图象与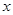 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为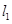 ,
,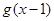 与
与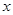 轴的交点N处的切线为
轴的交点N处的切线为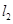 , 并且
, 并且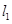 与
与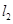 平行.
平行.(1)求
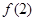 的值;
的值;(2)已知实数t∈R,求
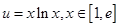 的取值范围及函数
的取值范围及函数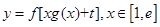 的最小值;
的最小值;(3)令
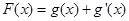 ,给定
,给定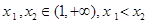 ,对于两个大于1的正数
,对于两个大于1的正数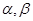 ,存在实数
,存在实数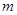 满足:
满足: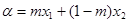 ,
,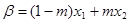 ,并且使得不等式
,并且使得不等式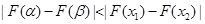 恒成立,求实数
恒成立,求实数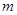 的取值范围.
的取值范围.(1)2 (2) (3)
(3)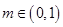
 (3)
(3)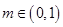
试题分析:
(1)根据题意求出f(x),g(x-1)与x轴交点的坐标,利用切线平行,即导函数在交点处的导函数值相等,即可求出f(x)中参数a的值,进而得到f(2).
(2)可以利用求定义域,求导,求单调性与极值 对比极值与端点值得到
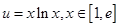 的取值范围
的取值范围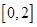 .进而直接用u替代
.进而直接用u替代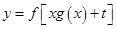 中的
中的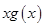 ,把问题转化为求解
,把问题转化为求解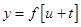 在区间
在区间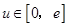 上的最小值,即为一个含参二次函数的最值.则利用二次函数的单调性,即分对称轴在区间
上的最小值,即为一个含参二次函数的最值.则利用二次函数的单调性,即分对称轴在区间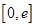 的左边,中,右边三种情况进行讨论得到函数
的左边,中,右边三种情况进行讨论得到函数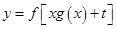 的最小值.
的最小值.(3)对F(x)求导求并确定导函数的符号得到函数F(x)的单调性,有了F(x)的单调性,则要得到不等式,我们只需要讨论m的范围确定
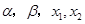 的大小关系,再根据单调性得到
的大小关系,再根据单调性得到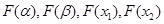 的大小关系,判断其是否符合不等式
的大小关系,判断其是否符合不等式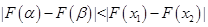 ,进而得到m的取值范围.
,进而得到m的取值范围.试题解析:
(1)
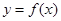 图象与
图象与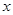 轴异于原点的交点
轴异于原点的交点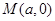 ,
,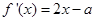 1分
1分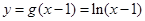 图象与
图象与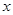 轴的交点
轴的交点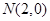 ,
,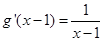 2分
2分由题意可得
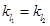 , 即
, 即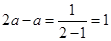
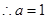 , 3分
, 3分∴
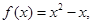 ,
,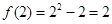 4分
4分(2)
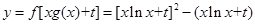 =
= 5分
5分令
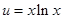 ,在
,在 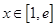 时,
时,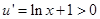 ,
,∴
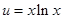 在
在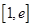 单调递增,
单调递增,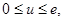 6分
6分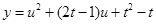 图象的对称轴
图象的对称轴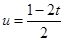 ,抛物线开口向上
,抛物线开口向上①当
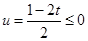 即
即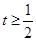 时,
时,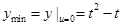 7分
7分②当
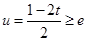 即
即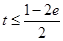 时,
时,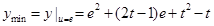 8分
8分③当
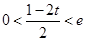 即
即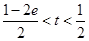 时,
时,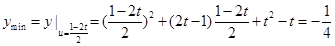 9分
9分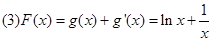 ,
,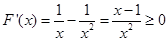
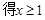
所以
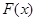 在区间
在区间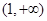 上单调递增
上单调递增 ∴
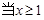 时,
时,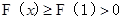 10分
10分①当
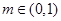 时,有
时,有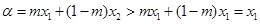 ,
,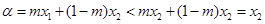 ,
,得
 ,同理
,同理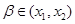 ,
, ∴ 由
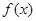 的单调性知
的单调性知 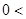
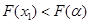
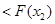 、
、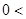
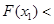
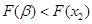
从而有
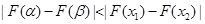 ,符合题设. 11分
,符合题设. 11分②当
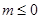 时,
时,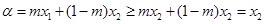 ,
,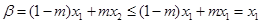 ,
,由
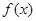 的单调性知
的单调性知 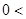
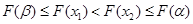 ,
,∴
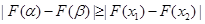 ,与题设不符 12分
,与题设不符 12分③当
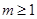 时,同理可得
时,同理可得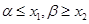 ,
,得
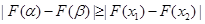 ,与题设不符. 13分
,与题设不符. 13分∴综合①、②、③得
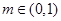 14分
14分
练习册系列答案
相关题目
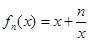 ,(
,(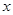 >0,
>0,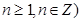 ,以点
,以点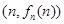 为切点作函数
为切点作函数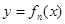 图象的切线
图象的切线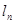 ,记函数
,记函数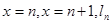 所围成的区域面积为
所围成的区域面积为 .
.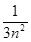 ;
;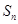 为数列
为数列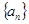 的前
的前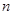 项和,求证:
项和,求证: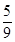 .来
.来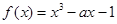 在区间[-1,1]上单调递减;
在区间[-1,1]上单调递减;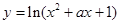 的定义域为R.若命题p或q为假命题,求
的定义域为R.若命题p或q为假命题,求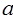 的取值范围.
的取值范围.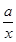 +ln x-1.
+ln x-1.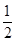 ,试讨论函数y=f(x)的单调性.
,试讨论函数y=f(x)的单调性.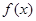 的导函数为
的导函数为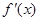 ,且满足关系式
,且满足关系式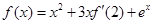 ,则
,则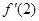 的值等于( )
的值等于( )