题目内容
已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”.下列函数中,有“巧值点”的是( )
①f(x)=x2;②f(x)=e-x;③f(x)=ln x;④f(x)=tan x;⑤f(x)=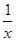 .
.
①f(x)=x2;②f(x)=e-x;③f(x)=ln x;④f(x)=tan x;⑤f(x)=
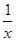 .
.| A.①③⑤ | B.③④ | C.②③④ | D.②⑤ |
A
①即x2=2x,这个方程显然有解,故①符合要求;②即e-x=-e-x,此方程无解,②不符合要求;③即ln x=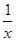 ,数形结合可知这个方程也存在实数解,符合要求;④中,f′(x)=
,数形结合可知这个方程也存在实数解,符合要求;④中,f′(x)=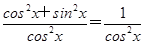 ,若f(x)=f′(x),即
,若f(x)=f′(x),即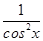 =tan x,化简得sin xcos x=1,即sin 2x=2,方程无解,④不符合要求;⑤中,f′(x)=-
=tan x,化简得sin xcos x=1,即sin 2x=2,方程无解,④不符合要求;⑤中,f′(x)=-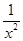 ,-
,-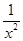 =
=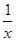 ,可得x=-1为该方程的解,故⑤符合要求.
,可得x=-1为该方程的解,故⑤符合要求.
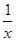 ,数形结合可知这个方程也存在实数解,符合要求;④中,f′(x)=
,数形结合可知这个方程也存在实数解,符合要求;④中,f′(x)=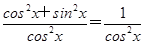 ,若f(x)=f′(x),即
,若f(x)=f′(x),即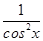 =tan x,化简得sin xcos x=1,即sin 2x=2,方程无解,④不符合要求;⑤中,f′(x)=-
=tan x,化简得sin xcos x=1,即sin 2x=2,方程无解,④不符合要求;⑤中,f′(x)=-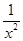 ,-
,-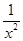 =
=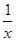 ,可得x=-1为该方程的解,故⑤符合要求.
,可得x=-1为该方程的解,故⑤符合要求.
练习册系列答案
相关题目
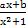 在点(-1,f(-1))处的切线方程为x+y+3=0.
在点(-1,f(-1))处的切线方程为x+y+3=0.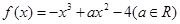 .
.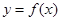 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为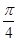 ,求
,求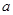 的值;
的值;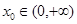 使
使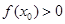 ,求
,求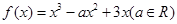 .
.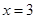 是
是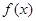 的极值点,求
的极值点,求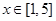 上的最大值;
上的最大值;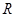 上的单调递增函数,求实数
上的单调递增函数,求实数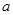 的取值范围.
的取值范围.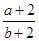 的取值范围是( )
的取值范围是( )
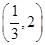
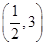
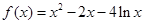 ,则
,则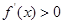 的解集为________.
的解集为________.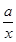 +ln x-1.
+ln x-1.