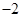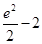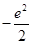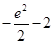题目内容
已知函数f(x)=-xln x+ax在(0,e)上是增函数,函数g(x)=|ex-a|+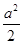 ,当x∈[0,ln 3]时,函数g(x)的最大值M与最小值m的差为
,当x∈[0,ln 3]时,函数g(x)的最大值M与最小值m的差为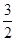 ,则a=________.
,则a=________.
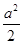 ,当x∈[0,ln 3]时,函数g(x)的最大值M与最小值m的差为
,当x∈[0,ln 3]时,函数g(x)的最大值M与最小值m的差为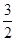 ,则a=________.
,则a=________.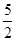
因为f′(x)=-ln x-1+a≥0在(0,e)上恒成立,所以a≥(ln x+1)max=2.
又x∈[0,ln 3]时,ex∈[1,3],所以当a∈(3,+∞)时,g(x)=a-ex+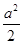 递减,此时M-m=a-1+
递减,此时M-m=a-1+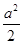 -
-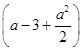 =2,不适合,舍去;当a∈[2,3]时,
=2,不适合,舍去;当a∈[2,3]时,
g(x)=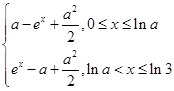 此时m=
此时m=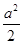 ,
,
Mmax=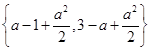 =a-1+
=a-1+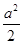 ,
,
所以a-1+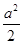 -
-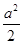 =a-1=
=a-1=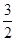 ,解得a=
,解得a=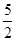 .
.
又x∈[0,ln 3]时,ex∈[1,3],所以当a∈(3,+∞)时,g(x)=a-ex+
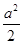 递减,此时M-m=a-1+
递减,此时M-m=a-1+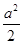 -
-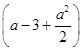 =2,不适合,舍去;当a∈[2,3]时,
=2,不适合,舍去;当a∈[2,3]时,g(x)=
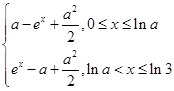 此时m=
此时m=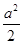 ,
,Mmax=
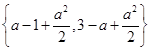 =a-1+
=a-1+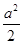 ,
,所以a-1+
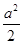 -
-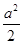 =a-1=
=a-1=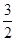 ,解得a=
,解得a=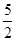 .
.
练习册系列答案
相关题目
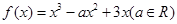 .
.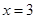 是
是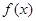 的极值点,求
的极值点,求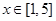 上的最大值;
上的最大值;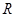 上的单调递增函数,求实数
上的单调递增函数,求实数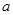 的取值范围.
的取值范围.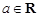 ,函数
,函数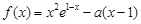 .
.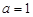 时,求
时,求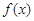 在
在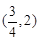 内的极大值;
内的极大值;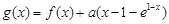 ,当
,当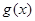 有两个极值点
有两个极值点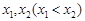 时,总有
时,总有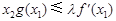 ,求实数
,求实数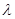 的值.(其中
的值.(其中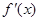 是
是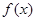 的导函数.)
的导函数.)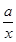 +ln x-1.
+ln x-1.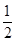 ,试讨论函数y=f(x)的单调性.
,试讨论函数y=f(x)的单调性.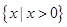
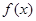 的导函数为
的导函数为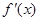 ,且满足关系式
,且满足关系式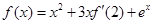 ,则
,则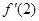 的值等于( )
的值等于( )