[题目]求下列函数的单调区间．(1)f(x)＝3|x|,(2)f(x)＝|x2+2x-3|．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】求下列函数的单调区间．

（1）f（x）＝3|x|；

（2）f（x）＝|x2＋2x－3|．

【答案】（1）减区间为(－∞，0]，增区间为[0，＋∞)；（2）增区间是[－3，－1]，[1，＋∞)；减区间是(－∞，－3]，[－1，1]．

【解析】

（1）化简函数为，作出函数的图象，即可求解；

（2）作出的图象，进而得到函数的图象，即可求解．

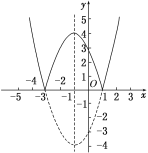
（1）由题意，函数，图象如图所示，

所以函数f（x）的单调递减区间为(－∞，0]，单调递增区间为[0，＋∞)．

（2）令，

作出的图象，保留其在x轴及x轴上方部分，把它在x轴下方的图象翻到x轴上方，

即可得到函数的图象，如图所示．

由图象易得：函数的递增区间是[－3，－1]，[1，＋∞)；

函数的递减区间是(－∞，－3]，[－1，1]．

练习册系列答案

相关题目

【题目】设函数．

（1）若是偶函数，求k的值；

（2）设不等式的解集为A，若，求实数m的取值范围；

（3）设函数，若g（x）在有零点，求实数的取值范围．

【题目】某学校为调查高三年级学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图（图1）和女生身高情况的频率分布直方图（图2）.已知图1中身高在170～175cm的男生人数有16人

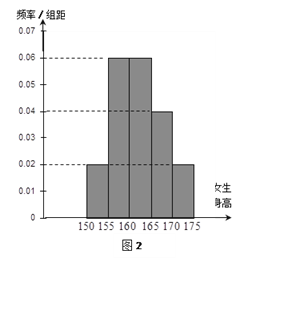
(1)根据频率分布直方图，完成下列的列联表，并判断能有多大（百分比）的把握认为“身高与性别有关”？

			总计
男生身高
女生身高
总计

(2)在上述80名学生中，从身高在170-175cm之间的学生按男、女性别分层抽样的方法，抽出5人，从这5人中选派3人当旗手，求3人中恰好有一名女生的概率.

	0.025	0.610	0.005	0.001
	5.024	4.635	7.879	10.828

参考公式及参考数据如下：

【题目】袋子中有5个大小质地完全相同的球，其中2个红球、3个黄球，从中不放回地依次随机摸出2个球，求下列事件的概率：

（1）A=“第一次摸到红球”；

（2）B=“第二次摸到红球”；

（3）AB=“两次都摸到红球”.

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，圆的方程为，直线的极坐标方程为.

(I )写出的极坐标方程和的平面直角坐标方程;

(Ⅱ) 若直线的极坐标方程为,设与的交点为与的交点为求的面积.

【题目】人的眼皮有单眼皮与双眼皮之分，这是由对应的基因决定的.生物学上已经证明：决定眼皮单双的基因有两种，一种是显性基因（记为），另一种是隐性基因（记为）；基因总是成对出现（如、、、），而成对的基因中，只要出现了显性基因，那么这个人就一定是双眼皮（也就是说，“单眼皮”的充要条件是“成对的基因是”）；如果不发生基因突变的话，成对的基因中，一个来自父亲，另一个来自母亲，但父母亲提供基因时都是随机的.有一对夫妻，两人成对的基因都是，不考虑基因突变，求他们的孩子是单眼皮的概率.