题目内容
由平面α外一点P引平面的三条相等的斜线段,斜足分别为A、B、C,O为△ABC的外心,求证:OP⊥α.
见解析
【解析】学生错【解析】
证明:因为O为△ABC的外心,所以OA=OB=OC,又因为PA=PB=PC,PO公用,所以△POA,△POB,△POC都全等,所以∠POA=∠POB=∠POC=90°,所以OP⊥α.
审题引导:要记OP⊥α,需记OP垂直于α内两条相交的直线,由图形易知,可考虑证OP垂直于△ABC的两条边,注意到图中的等腰三角形PBC、OBC,不准找到证题途径.
规范解答:证明:取BC的中点D,连结PD、OD,
∵PB=PC,OB=OC,∴BC⊥PD,BC⊥OD,(5分)
又PD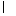 平面POD,OD?平面POD,且PD∩OD=D,∴BC⊥平面POD.(8分)
平面POD,OD?平面POD,且PD∩OD=D,∴BC⊥平面POD.(8分)
∵PO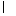 平面POD,∴BC⊥PO.
平面POD,∴BC⊥PO.
同理AB⊥PO.(12分)
又AB、BC是α内的两条相交直线,∴PO⊥α.(14分)
错解分析:上述解法中∠POA=∠POB=∠POC=90°,是对的,但它们为什么是直角呢?这里缺少必要的证明.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目