题目内容
已知：a、b、c、d是不共点且两两相交的四条直线，求证：a、b、c、d共面
见解析
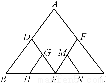
【解析】证法1：若当四条直线中有三条相交于一点，不妨设a、b、c相交于一点A，∴直线d和A确定一个平面α.又设直线d与a、b、c分别相交于E、F、G，则A、E、F、G∈α.∵A、E∈α，A、E∈a，∴a?α.同理可证b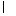
α，c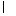α.∴a、b、c、d在同一平面α内．
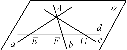
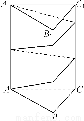
证法2：当四条直线中任何三条都不共点时，如图．∵这四条直线两两相交，则设相交直线a、b确定一个平面α.设直线c与a、b分别交于点H、K，则H、K∈α.又H、K∈c，∴c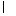α.同理可证d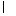α.∴a、b、c、d四条直线在同一平面α内．
练习册系列答案
相关题目
