题目内容
已知a、b、c都是正整数且abc=8,求证:log2(2+a)+log2(2+b)+log2(2+c)≥6.
【答案】分析:利用基本不等式,结合对数的运算法则,即可证得结论.
解答:证明:∵、b、c都是正整数,
∴ ,
,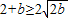 ,
,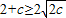
∵abc=8
∴(2+a)(2+b)(2+c)≥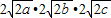 =8
=8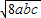 =64(当且仅当a=b=c=2时,等号成立)
=64(当且仅当a=b=c=2时,等号成立)
∴log2(2+a)+log2(2+b)+log2(2+c)≥log2(2+a)(2+b)(2+c)≥log264=6.
点评:本题考查不等式的证明,考查对数的运算法则,正确运用基本不等式是解题的关键.
解答:证明:∵、b、c都是正整数,
∴
 ,
,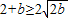 ,
,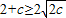
∵abc=8
∴(2+a)(2+b)(2+c)≥
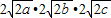 =8
=8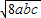 =64(当且仅当a=b=c=2时,等号成立)
=64(当且仅当a=b=c=2时,等号成立)∴log2(2+a)+log2(2+b)+log2(2+c)≥log2(2+a)(2+b)(2+c)≥log264=6.
点评:本题考查不等式的证明,考查对数的运算法则,正确运用基本不等式是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目