题目内容
设函数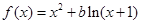 .
.
(1)若对定义域内任意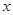 ,都有
,都有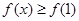 成立,求实数
成立,求实数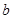 的值;
的值;
(2)若函数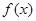 在定义域上是单调函数,求
在定义域上是单调函数,求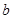 的范围;
的范围;
(3)若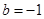 ,证明对任意正整数
,证明对任意正整数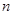 ,不等式
,不等式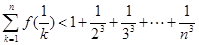 都成立.
都成立.
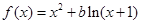 .
.(1)若对定义域内任意
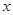 ,都有
,都有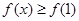 成立,求实数
成立,求实数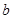 的值;
的值;(2)若函数
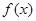 在定义域上是单调函数,求
在定义域上是单调函数,求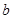 的范围;
的范围;(3)若
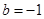 ,证明对任意正整数
,证明对任意正整数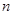 ,不等式
,不等式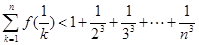 都成立.
都成立.(1)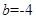 ;(2)
;(2)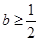 ;(3)当
;(3)当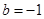 时,
时,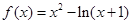
令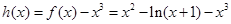 ,
,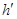
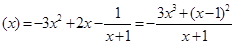 ,
,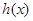 在
在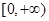 上递减 又
上递减 又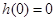 ,当
,当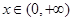 时,恒有
时,恒有 即
即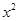
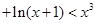 恒成立,当
恒成立,当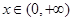 时,
时,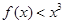 ,
,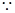
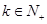 ,
,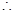
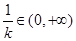
取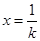
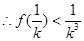
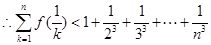 -
-
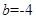 ;(2)
;(2)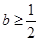 ;(3)当
;(3)当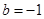 时,
时,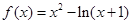
令
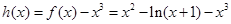 ,
,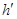
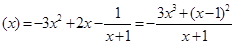 ,
,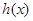 在
在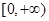 上递减 又
上递减 又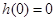 ,当
,当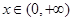 时,恒有
时,恒有 即
即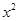
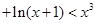 恒成立,当
恒成立,当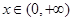 时,
时,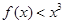 ,
,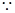
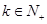 ,
,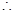
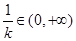
取
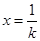
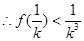
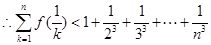 -
-试题分析:(1)
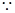
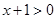
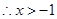
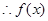 的定义域为
的定义域为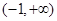 对
对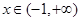 ,都有
,都有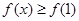 ,又函数
,又函数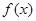 在定义域上连续.
在定义域上连续.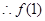 是函数
是函数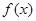 的最小值,
的最小值,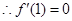
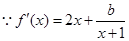 ,
,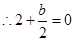
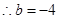 ………………4分
………………4分(2)

又
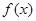 在定义域上单调,
在定义域上单调,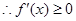 或
或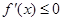 在
在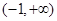 上恒成立,--5分
上恒成立,--5分若
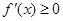 ,
, ,
,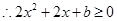 在
在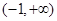 上恒成立,即
上恒成立,即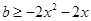 ,
,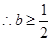 ----------7分
----------7分若
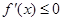 ,
, ,
,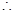
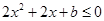 ,即
,即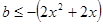 恒成立.
恒成立.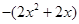 在
在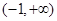 上无最小值.
上无最小值.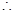 不存在
不存在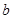 使
使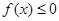 恒成立
恒成立综上,
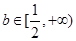 ……………9分
……………9分(3)当
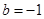 时,
时,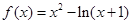
令
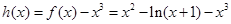 ,
,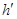
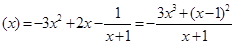
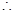 当
当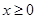 时,
时,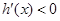
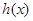 在
在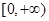 上递减
上递减 又
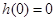 ,当
,当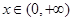 时,恒有
时,恒有 即
即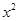
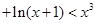 恒成立,
恒成立,当
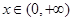 时,
时,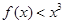 ,
,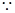
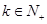 ,
,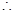
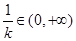
取
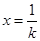
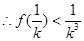
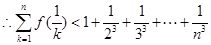 -------12分
-------12分点评:本题考查了利用导数研究函数的单调性以及函数与数列、不等式的综合的问题,属于难题.利用分类讨论思想和不等式放缩的技巧,是解决本题的关键,也是思考的难点.

练习册系列答案
相关题目
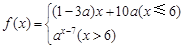 若数列{an}满足an=
若数列{an}满足an=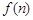 (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( )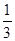 ,1)
,1)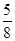 )
)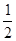 )
)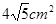 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽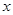 及长
及长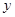 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.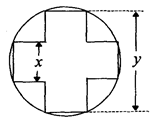
 在
在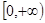 上是增函数,
上是增函数, 若
若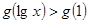 ,则
,则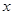 的取值范围是( )
的取值范围是( )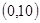
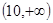

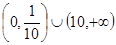
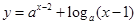 +1(a>0,a≠1)的图象必经过定点 ( )
+1(a>0,a≠1)的图象必经过定点 ( )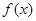 满足
满足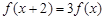 ,当
,当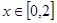 时,
时,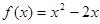 ,若
,若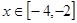 时,
时,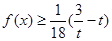 恒成立,则实数
恒成立,则实数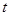 的取值范围是 .
的取值范围是 .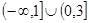
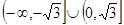
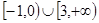
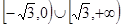
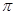 x(-2≤x≤4)的图像所有交点的横坐标之和等于
x(-2≤x≤4)的图像所有交点的横坐标之和等于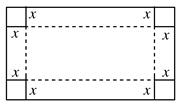
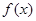 ,并指出函数
,并指出函数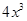 立方米的同时,又使得底面积最大,求x的值.
立方米的同时,又使得底面积最大,求x的值.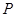 (元)之间的关系为
(元)之间的关系为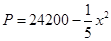 ,且生产
,且生产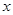 吨的成本为
吨的成本为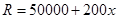 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)